已知圆O：x2+y2=2，直线l：x+2y-4=0，点P（x0，y0）在直线l上．若存在圆C上的点Q，使得∠OPQ=45°（O为坐标原点），则x0的取值范围是（）A.[0，1]B.[0，85]C.[-12，1]D.[-12，85]

Question

已知圆O：x²+y²=2，直线l：x+2y-4=0，点P（x₀，y₀）在直线l上．若存在圆C上的点Q，使得∠OPQ=45°（O为坐标原点），则x₀的取值范围是（　　）

A. [0，1]

B. [0，

(8)/(5)]

C. [-

(1)/(2)，1]

D. [-

(1)/(2)，(8)/(5)]

Answer 1

圆O外有一点P，圆上有一动点Q，∠OPQ在PQ与圆相切时取得最大值．
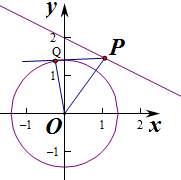
如果OP变长，那么∠OPQ可以获得的最大值将变小．可以得知，当∠OPQ=45°，且PQ与圆相切时，PO=2，
而当PO>2时，Q在圆上任意移动，∠OPQ<45°恒成立0．
因此满足PO≤2，就能保证一定存在点Q，使得∠OPQ=45°，否则，这样的点Q是不存在的；
∵点P（x₀，y₀）在直线x+2y-4=0上，∴x₀+2y₀-4=0，即y₀=(4-x0)/(2)
∵|OP|²=x₀²+y₀²=x₀²+（(4-x0)/(2)）²=(5)/(4)x₀²-2x₀+4≤4，
∴(5)/(4)x₀²-2x₀≤0，
解得，0≤x₀≤(8)/(5)，
∴x₀的取值范围是[0，(8)/(5)]
故选：B