早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.(1)求二次函数y=ax2+bx+c的表达式;(2)过点A作AC平行于x轴,交抛物线于点C,
题目详情
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
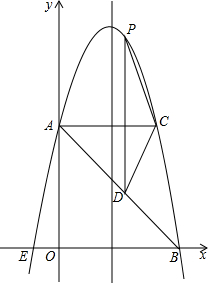
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行与y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.

(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行与y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
▼优质解答
答案和解析
(1)设抛物线解析式为y=a(x-2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=-1,
y=-(x-2)2+9=-x2+4x+5,
(2)当y=0时,-x2+4x+5=0,
∴x1=-1,x2=5,
∴E(-1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=-1,n=5,
∴直线AB的解析式为y=-x+5;
设P(x,-x2+4x+5),
∴D(x,-x+5),
∴PD=-x2+4x+5+x-5=-x2+5x,
∵AC=4,
∴S四边形APCD=
×AC×PD=2(-x2+5x)=-2x2+10x,
∴当x=-
=
时,
∴S四边形APCD最大=
,
(3)如图,
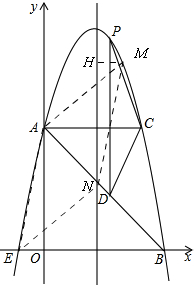
过M作MH垂直于对称轴,垂足为H,
∵MN∥AE,MN=AE,
∴△HMN≌△AOE,
∴HM=OE=1,
∴M点的横坐标为x=3或x=1,
当x=1时,M点纵坐标为8,
当x=3时,M点纵坐标为8,
∴M点的坐标为M1(1,8)或M2(3,8),
∵A(0,5),E(-1,0),
∴直线AE解析式为y=5x+5,
∵MN∥AE,
∴MN的解析式为y=5x+b,
∵点N在抛物线对称轴x=2上,
∴N(2,10+b),
∵AE2=OA2+0E2=26
∵MN=AE
∴MN2=AE2,
∴MN2=(2-1)2+[8-(10+b)]2=1+(b+2)2
∵M点的坐标为M1(1,8)或M2(3,8),
∴点M1,M2关于抛物线对称轴x=2对称,
∵点N在抛物线对称轴上,
∴M1N=M2N,
∴1+(b+2)2=26,
∴b=3,或b=-7,
∴10+b=13或10+b=3
∴当M点的坐标为(1,8)时,N点坐标为(2,13),
当M点的坐标为(3,8)时,N点坐标为(2,3),
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=-1,
y=-(x-2)2+9=-x2+4x+5,
(2)当y=0时,-x2+4x+5=0,
∴x1=-1,x2=5,
∴E(-1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=-1,n=5,
∴直线AB的解析式为y=-x+5;
设P(x,-x2+4x+5),
∴D(x,-x+5),
∴PD=-x2+4x+5+x-5=-x2+5x,
∵AC=4,
∴S四边形APCD=
| 1 |
| 2 |
∴当x=-
| 10 |
| 2×(-2) |
| 5 |
| 2 |
∴S四边形APCD最大=
| 25 |
| 2 |
(3)如图,

过M作MH垂直于对称轴,垂足为H,
∵MN∥AE,MN=AE,
∴△HMN≌△AOE,
∴HM=OE=1,
∴M点的横坐标为x=3或x=1,
当x=1时,M点纵坐标为8,
当x=3时,M点纵坐标为8,
∴M点的坐标为M1(1,8)或M2(3,8),
∵A(0,5),E(-1,0),
∴直线AE解析式为y=5x+5,
∵MN∥AE,
∴MN的解析式为y=5x+b,
∵点N在抛物线对称轴x=2上,
∴N(2,10+b),
∵AE2=OA2+0E2=26
∵MN=AE
∴MN2=AE2,
∴MN2=(2-1)2+[8-(10+b)]2=1+(b+2)2
∵M点的坐标为M1(1,8)或M2(3,8),
∴点M1,M2关于抛物线对称轴x=2对称,
∵点N在抛物线对称轴上,
∴M1N=M2N,
∴1+(b+2)2=26,
∴b=3,或b=-7,
∴10+b=13或10+b=3
∴当M点的坐标为(1,8)时,N点坐标为(2,13),
当M点的坐标为(3,8)时,N点坐标为(2,3),
看了 如图,在平面直角坐标系中,抛...的网友还看了以下:
如图所示,正比例函数y=ax的图像与反比例函数y=k/x的图像交于点A(3,2)M(m,n)是反比 2020-04-08 …
的图象交于点A(3,2)(1)求上述两函数的表达式;(2)M(m,n)是反比例函数图象上的一个动点 2020-04-08 …
excel2007怎么调X坐标轴上的数值位置,使其下移到底部?由于纵坐标轴的0值点在中心 横坐 2020-05-16 …
如图1,已知直线EA与x轴、y轴分别交于点E和点A(0,2),过直线EA上的两点F、G分别作轴的垂 2020-06-12 …
坐标轴上的点的集合表示为?内有题坐标轴上的点的集合可以表示为A.{(x,y)|x=0,y≠0或x≠ 2020-06-14 …
在平面直角坐标系xOy中,点P和点P'关于y=x轴对称,点Q和点P'关于R(a,0)中心对称,则称 2020-06-19 …
小明在学习了平面直角坐标系后,突发奇想,画出了这样的图形(如图),他把图形与x轴正半轴的交点依次记 2020-07-09 …
如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-2,0),(-1,0),BC⊥x 2020-08-02 …
在0≤x≤pi的范围内求曲线y=sinx与x轴围成的面积。0到pi就是曲线的半个周期。假如我把这个波 2020-12-15 …
一道作业中的2011哈尔滨中考题,在平面直角坐标系中,点0是坐标原点,四边形ABCD为菱形,AB边在 2021-01-22 …