早教吧作业答案频道 -->数学-->
如图,直线l:y=-3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+4(a<0)经过点B.(1)求a的值,并写出抛物线的表达式;(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,
题目详情
如图,直线l:y=-3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+4(a<0)经过点B.
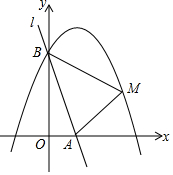
(1)求a的值,并写出抛物线的表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)经直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,请直接写出此时AC的值.

(1)求a的值,并写出抛物线的表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)经直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,请直接写出此时AC的值.
▼优质解答
答案和解析
(1)把x=0代入y=-3x+3得y=3,
∴B(0,3),
把B(0,3)代入y=ax2-2ax+a+4,
∴3=a+4,
∴a=-1,
∴y=-x2+2x+3,
(2)令y=0代入得:0=-x2+2x+3,
∴x=-1或3,
∴抛物线与x轴的交点横坐标为-1和3,
∵M在抛物线上,且在第一象限内,
∴0令y=0代入y=-3x+3,
∴x=1,
∴A的坐标为(1,0),
由题意知:M的坐标为(m,-m2+2m+3),
S=S四边形OAMB-S△AOB
=S△OBM+S△OAM-S△AOB
=
×m×3+
×1×(-m2+2m+3)-
×1×3
=-
m2+
m
=-
(m-
)2+
∴当m=
时,S取得最大值
;
(3)①由(2)可知:
当m=
时,y=-(
)2+2×
+3=
,
∴M′的坐标为(
,
);
②如图,
过B点作BD 垂直于l′于D点,过M′点作M′E垂直于l′于E点,
垂直于l′于D点,过M′点作M′E垂直于l′于E点,
则BD=d1,M′E=d2,
∵S△ABM′=
×AC×(d1+d2)
当d1+d2取得最大值时,AC取得最小值,
∴AC⊥B M′时,AC取得最小值.
∵B(0,3)和M′(
,
)
∴BM′=
,
∵S△ABM′=
×AC×BM′=
,
∴AC=
.
∴B(0,3),
把B(0,3)代入y=ax2-2ax+a+4,
∴3=a+4,
∴a=-1,
∴y=-x2+2x+3,
(2)令y=0代入得:0=-x2+2x+3,
∴x=-1或3,
∴抛物线与x轴的交点横坐标为-1和3,
∵M在抛物线上,且在第一象限内,
∴0
∴x=1,
∴A的坐标为(1,0),
由题意知:M的坐标为(m,-m2+2m+3),
S=S四边形OAMB-S△AOB
=S△OBM+S△OAM-S△AOB
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 5 |
| 2 |
=-
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 8 |
∴当m=
| 5 |
| 2 |
| 25 |
| 8 |
(3)①由(2)可知:
当m=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 7 |
| 4 |
∴M′的坐标为(
| 5 |
| 2 |
| 7 |
| 4 |
②如图,
过B点作BD
 垂直于l′于D点,过M′点作M′E垂直于l′于E点,
垂直于l′于D点,过M′点作M′E垂直于l′于E点,则BD=d1,M′E=d2,
∵S△ABM′=
| 1 |
| 2 |
当d1+d2取得最大值时,AC取得最小值,
∴AC⊥B M′时,AC取得最小值.
∵B(0,3)和M′(
| 5 |
| 2 |
| 7 |
| 4 |
∴BM′=
5
| ||
| 4 |
∵S△ABM′=
| 1 |
| 2 |
| 25 |
| 8 |
∴AC=
| 5 |
看了 如图,直线l:y=-3x+3...的网友还看了以下:
抛物线过a(4,0)b(1,0)c(0,4)p在抛物线上1求解析式2是否有一点p使acp以ac为直 2020-05-13 …
(2010•崇明县二模)已知:如图,AC=BC,∠ACB=90°,点B的坐标为(1,0),抛物线过 2020-05-17 …
抛物线过A(-1,1)B(3,1)且最小值为-3,求此抛物线的解析式 2020-05-22 …
抛物线过A(-1,1)B(3,1)且最小值为-3,求此抛物线的解析式 2020-05-22 …
直线过A(1,0)且与抛物线y∧2=-2x仅有一个公共点,这样的直线共有几条?直线过A(1,0)且 2020-06-03 …
在平面坐标系中抛物线过A(-4,0)B(0,-4)C(2,0)三点点M第三象限内抛物线上动点,点M 2020-06-14 …
直线过A(3,4),B(4,0)两点,现直线绕A点顺时针旋转45度,问所得新的直线函数关系式 2020-06-20 …
(2014•义乌市)如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=O 2020-06-29 …
圆的切线割线方程若有一点A(x0,y0),圆(x-a)^2+(y-b)^2=r^2直线过A与圆相切 2020-07-22 …
已知抛物线过A(-2,0)、B(1,0)、C(0,2)三点,(1)求这条抛物线的解析式;(2)在这 2020-08-01 …