早教吧作业答案频道 -->数学-->
如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.(1)若∠AOB=45,OM=4,OQ=2,求证:CN⊥OB;(2)当点N在边OB上
题目详情
如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点 Q,PM∥OB交OA于点M.
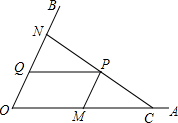
(1)若∠AOB=45,OM=4,OQ=2,求证:CN⊥OB;
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:
-
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由;
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求
的取值范围.

(1)若∠AOB=45,OM=4,OQ=2,求证:CN⊥OB;
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:
| 1 |
| OM |
| 1 |
| ON |
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求
| S1 |
| S2 |
▼优质解答
答案和解析
(1)如图1,
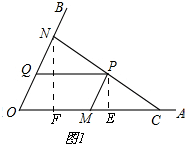
过P作PE⊥OA于E,NF⊥OA,
∵PQ∥OA,PM∥OB,
∴四边形OMPQ为平行四边形,
∴PM=OQ=
,∠PME=∠AOB=45°,
∴PE=PMsin45°=1,ME=1,
∴CE=OC-OM-ME=1,
∴tan∠PCE=
=1,
∴∠PCE=45°,
∴∠CNO=90°,
∴CN⊥OB;
(2)①
-
的值不发生变化,
理由:设OM=x,ON=y,
∵四边形OMPQ为菱形,
∴OQ=QP=OM=x,NQ=y-x,
∵PQ∥OA,
∴∠NQP=∠O,
∵∠QNP=∠ONC,
∴△NQP∽△NOC,
∴
=
,
∴
=
,
∴6y-6x=xy,
∴
-
=
,
∴
-
=
;
②如图2,
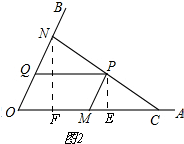
过P作PE⊥OA,过N作NF⊥OA,
∴S1=OM×PE,S2=
OC×NF,
∴
=
,
∵PM∥OB,
∴∠PMC=∠O∠,
∵∠PCM=∠NCO,
∴△CPM∽△CNO,
∴
=
=
,
∴
=
,
∵0<x<6,
∴0<
<
.

过P作PE⊥OA于E,NF⊥OA,
∵PQ∥OA,PM∥OB,
∴四边形OMPQ为平行四边形,
∴PM=OQ=
| 2 |
∴PE=PMsin45°=1,ME=1,
∴CE=OC-OM-ME=1,
∴tan∠PCE=
| PE |
| CE |
∴∠PCE=45°,
∴∠CNO=90°,
∴CN⊥OB;
(2)①
| 1 |
| OM |
| 1 |
| ON |
理由:设OM=x,ON=y,
∵四边形OMPQ为菱形,
∴OQ=QP=OM=x,NQ=y-x,
∵PQ∥OA,
∴∠NQP=∠O,
∵∠QNP=∠ONC,
∴△NQP∽△NOC,
∴
| OP |
| OC |
| NQ |
| NO |
∴
| x |
| 6 |
| y-x |
| y |
∴6y-6x=xy,
∴
| 1 |
| x |
| 1 |
| y |
| 1 |
| 6 |
∴
| 1 |
| OM |
| 1 |
| ON |
| 1 |
| 6 |
②如图2,

过P作PE⊥OA,过N作NF⊥OA,
∴S1=OM×PE,S2=
| 1 |
| 2 |
∴
| S1 |
| S2 |
| xPE |
| 3NF |
∵PM∥OB,
∴∠PMC=∠O∠,
∵∠PCM=∠NCO,
∴△CPM∽△CNO,
∴
| PE |
| NF |
| CM |
| CO |
| 6-x |
| 6 |
∴
| S1 |
| S2 |
| x(6-x) |
| 18 |
∵0<x<6,
∴0<
| S1 |
| S2 |
| 1 |
| 2 |
看了 如图,C为∠AOB的边OA上...的网友还看了以下:
如图,在平面直角坐标系xOy中,已知A(9,0)、B(9,12),点M、N分别是线段OB、AB上的 2020-06-14 …
已知数轴上三点M,O,N对应的数分别为-3,0,1,点P为数轴上任意一点,其对应的数为x.(1)如 2020-07-19 …
如图,1,2,3,4,分别是圆o的内接正三角形,正方形,正五边形,.正n边形,点m,n分别从点bc 2020-07-21 …
如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCD 2020-07-21 …
如图所示,M、N和P是以MN为直径的半圆弧上的三点,O点为半圆弧的圆.电荷量相等、符号相反的两个点 2020-07-29 …
如图,P和Q为带电量分别为+q和-q的两个等量异种电荷,两者相距为L,O为PQ连线的中点,M、N为 2020-08-01 …
如图,M是以AB为直径的⊙O内的一点,AM,BM的延长线分别与圆O交于点C,D,过点M作MN⊥AB于 2020-11-01 …
(2014•大连二模)如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经 2020-12-05 …
已知A为⊙O上一点,B为⊙A与OA的交点,⊙A与⊙O的半径分别为r、R,且r<R.(Ⅰ)如图1,过点 2021-01-11 …
在数轴上,点m、o、n分别表示-3,0,1,点p为数轴上任意一点,其对应数为x.如果点p以每分钟三个 2021-01-12 …