如图12-1，⊙O是等边三角形ABC的外接圆，点P是⊙O上一点，连结CP、AP作射线BP．（1）求证：PC平分∠APB；（2）试猜想线段PA，PB，

Question

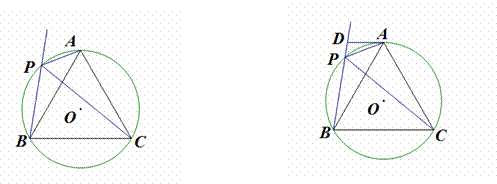
如图 12-1 ， ⊙O 是等边三角形 ABC 的外接圆，点 P 是 ⊙O 上一点，连结 CP 、 AP 作射线 BP ．

（ 1 ）求证： PC 平分 ∠APB ；

（ 2 ）试猜想线段 PA ， PB ， PC 之间的数量关系，并证明你的结论；

（ 3 ）如图 12-2 ，过点 A 做 ⊙O 的切线交射线 BP 于点 D. 若 AD= 2 ， PD= 1 ，求 ⊙O 的半径．

Answer 1

（ 1 ） ∵ 三角形 ABC 是等边三角形

∴ ∠BAC=∠ABC=∠ACB=60°……………………………………………… 1 分

∵ ⊙O 是等边三角形 ABC 的外接圆，点 P 是 ⊙O 上一点，

∴ ∠BPC=∠BAC ∠APC=∠ABC…………………………………………… 2 分

∴ ∠BPC= ∠APC

∴ PC 平分 ∠APB……………………………………………………………… 3 分

（ 2 ） PA + PB = PC ， …………………………………………………………… ……… 4 分

证明：在线段 PC 上截取 PF = PB ，连接 BF ，

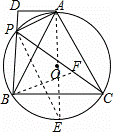∵ PF = PB ， ∠ BPC =60° ，

∴△ PBF 是等边三角形，

∴ PB = BF ， ∠ BFP =60° ，

∴∠ BFC =180° ﹣ ∠ PFB =120° ，

∵∠ BPA =∠ APC +∠ BPC =120° ，

∴∠ BPA =∠ BFC ， …………………………………………………… 5 分

在 △ BPA 和 △ BFC 中， ，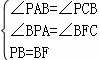

∴△ BPA ≌△ BFC （ AAS ），

∴ PA = FC ， AB = BC ，

∴ PA + PB = PF + FC = PC ；    …………………………………………………… 6 分

（其它证明方法按步骤酌情给分）

（ 3 ）作 ⊙ O 的直径 AE ，连接 PE ，

AE 是 ⊙ O 的直径， AD 是 ⊙ O 的切线，

∠ DAE =∠ APE =90° ，

∴∠ PAD +∠ PAE =∠ PAE +∠ E =90° ，

∴∠ PAD =∠ E ，

∵∠ PBA =∠ E ， ∴∠ PAD =∠ PBA ，

∵∠ PAD =∠ PBA ， ∠ ADP =∠ BDA ，

∴△ ADP ∽△ BDA ，

∴ = = ，

∵ AD =2 ， PD =1

∴ BD =4 ， AB =2 AP ，

∴ BP = BD ﹣ DP =3 ， ……………………………………………………………… 7 分

∵∠ APD =180° ﹣ ∠ BPA =60° ，

∴∠ APD =∠ APC ，

∵∠ PAD =∠ E ， ∠ PCA =∠ E ，

∴∠ PAD =∠ PCA ，

∴△ ADP ∽△ CAP ， ………………………………………………… …………… 8 分

∴ = ，

∴ AP ² = CP • PD ，

∴ AP ² = （ 3+ AP ） •1 ，

解得： AP = 或 AP = （舍去），

∴ BC = AB =2 AP =1+ ． ……………………………………………………………… 9 分

∴⊙ O 的半径为 …………………………………… 10 分