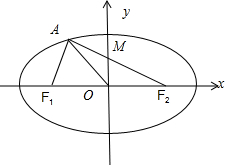
已知椭圆C：x2a2+y2b2=1（a>b>0）的右焦点为F2，O为坐标原点，M为y轴上一点，点A是直线MF2与椭圆C的一个交点，且|OA|=|OF2|=2|OM|，则椭圆C的离心率为（）A.13B.25C.55D.53

Question

已知椭圆C：

(x2)/(a2)+(y2)/(b2)=1（a>b>0）的右焦点为F₂，O为坐标原点，M为y轴上一点，点A是直线MF₂与椭圆C的一个交点，且|OA|=|OF₂|=2|OM|，则椭圆C的离心率为（　　）

A.

(1)/(3)

B.

(2)/(5)

C.

(√(5))/(5)

D.

(√(5))/(3)

Answer 1

如图，取椭圆的左焦点为F₁，连接AF₁，
依题意：|OA|=|OF₂|=2|OM|=c，可得∠F1AF2=900．
△F₁AF₂∽△MOF₂，⇒(AF1)/(AF2)=(OM)/(OF2)=(1)/(2)，
∵AF₁+AF₂=2a，∴AF1=(2a)/(3)，AF2=(4a)/(3)．
由AF12+AF22=F1F22⇒((2a)/(3))2+((4a)/(3))2=(2c)2
(c2)/(a2)=(5)/(9)，∴e=(c)/(a)=(√(5))/(3)．
则椭圆C的离心率为：(√(5))/(3)，
故选：D