如图1，在△ABC中，∠ACB=90°，BC=2，∠A=30°，点E，F分别是线段BC，AC的中点，连结EF．（1）线段BE与AF的位置关系是

Question

如图 1 ，在 △ ABC 中， ∠ ACB=90 ° ， BC=2 ， ∠ A=30 ° ，点 E ， F 分别是线段 BC ， AC 的中点，连结 EF ．

（ 1 ）线段 BE 与 AF 的位置关系是 　 　 ， = 　 ．

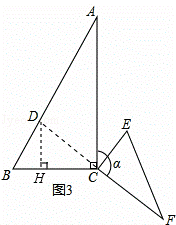
（ 2 ）如图 2 ，当 △ CEF 绕点 C 顺时针旋转 a 时（ 0 ° ＜ a ＜ 180 ° ），连结 AF ， BE ，（ 1 ）中的结论是否仍然成立．如果成立，请证明；如果不成立，请说明理由．

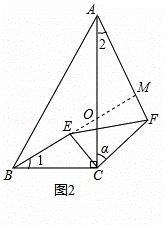
（ 3 ）如图 3 ，当 △ CEF 绕点 C 顺时针旋转 a 时（ 0 ° ＜ a ＜ 180 ° ），延长 FC 交 AB 于点 D ，如果 AD=6 ﹣ 2 ，求旋转角 a 的度数．

Answer 1

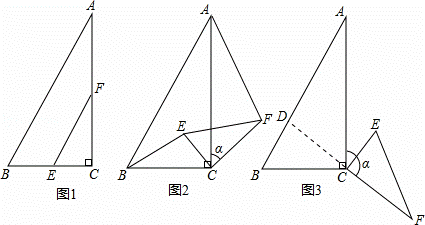
（ 1 ）如图 1 ，线段 BE 与 AF 的位置关系是互相垂直；

∵∠ ACB=90 ° ， BC=2 ， ∠ A=30 ° ，

∴ AC=2 ，

∵ 点 E ， F 分别是线段 BC ， AC 的中点，

∴ = ；

故答案为：互相垂直； ；

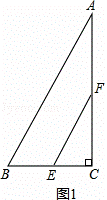
（ 2 ）（ 1 ）中结论仍然成立．

证明：如图 2 ， ∵ 点 E ， F 分别是线段 BC ， AC 的中点，

∴ EC= BC ， FC= AC ，

∴ = = ，

∵∠ BCE= ∠ ACF= α ，

∴△ BEC ∽△ AFC ，

∴ = = = ，

∴∠ 1= ∠ 2 ，

延长 BE 交 AC 于点 O ，交 AF 于点 M

∵∠ BOC= ∠ AOM ， ∠ 1= ∠ 2

∴∠ BCO= ∠ AMO=90 °

∴ BE ⊥ AF ；

（ 3 ）如图 3 ， ∵∠ ACB=90 ° ， BC=2 ， ∠ A=30 °

∴ AB=4 ， ∠ B=60 °

过点 D 作 DH ⊥ BC 于 H

∴ DB=4 ﹣（ 6 ﹣ 2 ） =2 ﹣ 2 ，

∴ BH= ﹣ 1 ， DH=3 ﹣ ，

又 ∵ CH=2 ﹣（ ﹣ 1 ） =3 ﹣ ，

∴ CH=DH ，

∴∠ HCD=45 ° ，

∴∠ DCA=45 ° ，

∴α =180 ° ﹣ 45 ° =135 ° ．