早教吧作业答案频道 -->数学-->
点O为直线AB上一点,在直线AB上侧任作一个∠COD,使得∠COD=90°.(1)如图1,过点O作射线OE,当OE恰好为∠AOD的角平分线时,请直接写出∠BOD与∠COE之间的倍数关系,即∠BOD=∠COE(填一
题目详情
点O为直线AB上一点,在直线AB上侧任作一个∠COD,使得∠COD=90°.
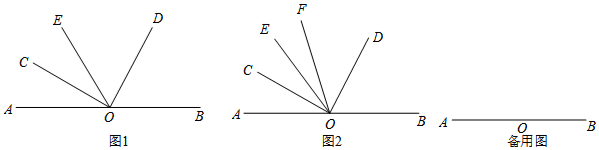
(1)如图1,过点O作射线OE,当OE恰好为∠AOD的角平分线时,请直接写出∠BOD与∠COE之间的倍数关系,即∠BOD=___∠COE(填一个数字);
(2)如图2,过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,求∠FOB+∠EOC的度数;
(3)在(2)的条件下,若∠EOC=3∠EOF,求∠AOE的度数.
(1)如图1,过点O作射线OE,当OE恰好为∠AOD的角平分线时,请直接写出∠BOD与∠COE之间的倍数关系,即∠BOD=___∠COE(填一个数字);
(2)如图2,过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,求∠FOB+∠EOC的度数;
(3)在(2)的条件下,若∠EOC=3∠EOF,求∠AOE的度数.

▼优质解答
答案和解析
(1)∠BOD=2∠COE;理由如下:
∵∠COD=90°.
∴∠BOD+∠AOC=90°,
∵OE平分∠AOD,
∴∠AOE=∠DOE=
∠AOD,
又∵∠BOD=180°-∠AOD,
∴∠COE=∠AOE-∠AOC=
∠AOD-(90°-∠BOD)=
(180°-∠BOD)-90°+∠BOD=
∠BOD,
∴∠BOD=2∠COE;
故答案为:2;
(2)∵OC为∠AOE的角平分线,OF平分∠COD,
∴∠AOC=∠COE,∠COF=∠DOF=45°,
∴∠FOB+∠EOC=∠DOF+∠BOD+∠AOC=45°+90°=135°;
(3)∵∠EOC=3∠EOF,
设∠EOF=x,则∠EOC=3x,
∴∠COF=4x,由(2)得:∠AOE=2∠COE=6x,∠DOF=4x,
∵∠COD=90°,
∴4x+4x=90°,
解得:x=11.25°,
∴∠AOE=6×11.25°=67.5°.
∵∠COD=90°.
∴∠BOD+∠AOC=90°,
∵OE平分∠AOD,
∴∠AOE=∠DOE=
| 1 |
| 2 |
又∵∠BOD=180°-∠AOD,
∴∠COE=∠AOE-∠AOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOD=2∠COE;
故答案为:2;
(2)∵OC为∠AOE的角平分线,OF平分∠COD,
∴∠AOC=∠COE,∠COF=∠DOF=45°,
∴∠FOB+∠EOC=∠DOF+∠BOD+∠AOC=45°+90°=135°;
(3)∵∠EOC=3∠EOF,
设∠EOF=x,则∠EOC=3x,
∴∠COF=4x,由(2)得:∠AOE=2∠COE=6x,∠DOF=4x,
∵∠COD=90°,
∴4x+4x=90°,
解得:x=11.25°,
∴∠AOE=6×11.25°=67.5°.
看了 点O为直线AB上一点,在直线...的网友还看了以下:
如图1,在平行四边形ABCD中,AE⊥BC于点E,E恰为BC的中点,tanB=2.;(3)请你在图 2020-05-13 …
在如图所示的五个方格中的字母都表示数字,中间一行的三个数字从左到右组成的三位数100d+10b+e 2020-05-13 …
已知函数f(x)=(x-k)²e∧(x/k).(1)若方程f(x)=1/e恰有两个不同的解,求实已 2020-06-27 …
整数9可以表示成两个连续正整数之和:9=4+5;此外,9还恰可以用两种方法表示成正整数之和:9=4 2020-06-27 …
如图,将平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,其中点B、C、D分别落在点E、F、 2020-07-20 …
初一平行线2点20分,时针和分针所成的角是()如果钟面上时针和分针恰成90°的角,那么时针所指的时候 2020-11-03 …
数学学得好的进来帮忙!最近网上看一个图片,填空的,内容是A+B-9=4,C-D*E=4,F+G-H= 2020-11-04 …
一道推理题求ABCDFGHI分别代表0-9的那个数字?AB*C=C^EE*F=HFG*D=GD-HH 2020-11-21 …
一道算数题设一个数为A(A为1-9其中一数)A+3-2=BB×9=C将C的个位和十位相加=DD×50 2020-11-23 …
同学们熟悉的e度论坛网址是bbs.eduu.com,如果令每个字母代表0到9中的一个数字(相同字母代 2020-12-23 …