早教吧作业答案频道 -->数学-->
已知线段BB′=4,直线l垂直平分BB′,交BB′于点O,在属于l并且以O为起点的同一射线上取两点P、P′,使OP•OP′=9,建立适当的坐标系,求直线BP与直线B′P′的交点M的轨迹方程.
题目详情
已知线段BB′=4,直线l垂直平分BB′,交BB′于点O,在属于l并且以O为起点的同一射线上取两点P、P′,使OP•OP′=9,建立适当的坐标系,求直线BP与直线B′P′的交点M的轨迹方程.
▼优质解答
答案和解析
以O为原点,BB′为yy轴,l为xxx轴建立如图所示直角坐标系,则B(0,2),B′(0,-2),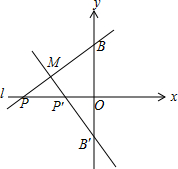
设P(a,0),a≠0,则由OP•OP′=9,得P′(
,0),
直线BP的方程为
+
=1,即2x+ay-2a=0,
直线B′P′的方程为
+
=1,即2ax-9y-18=0.
设M(x,y),联立
,解得
,
消去a,可得4x2+9y2=36(x≠0).
∴点M的轨迹是长轴长为6,短轴长为4的椭圆(除去点B、B′).

设P(a,0),a≠0,则由OP•OP′=9,得P′(
| 9 |
| a |
直线BP的方程为
| x |
| a |
| y |
| 2 |
直线B′P′的方程为
| x | ||
|
| y |
| -2 |
设M(x,y),联立
|
|
消去a,可得4x2+9y2=36(x≠0).
∴点M的轨迹是长轴长为6,短轴长为4的椭圆(除去点B、B′).
看了 已知线段BB′=4,直线l垂...的网友还看了以下:
如图所示,金属棒a从高为h处自静止起沿光滑的弧形导轨下滑,进入光滑导轨的水平部分,导轨的水平部分处于 2020-03-30 …
如图所示,水平面内有一平行金属导轨,导轨光滑且电阻不计,匀强磁场与导轨平面垂直阻值为R的导体棒垂直 2020-04-13 …
如图所示,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,二者平滑 2020-05-13 …
在平面直角坐标系xOy中,已知动点M(x,y)和N(-4,y)满足OM⊥ON.(1)求动点M的轨迹 2020-05-13 …
关于丙二烯.丁三稀的轨道杂化以及分子结构我认为前面一个是2个ll2.2π键,因为中间的C有两个垂直 2020-07-21 …
如图所示,水平面内有一平行金属导轨,导轨光滑且电阻不计.匀强磁场与导轨平面垂直.阻值为R的导体棒垂 2020-07-29 …
在平面直角坐标系中xoy中,点F为(1,0),直线l为x=-1,P为平面上的动点,过点P做直线l的 2020-07-29 …
给一组过定点的直线系和一个定圆咋样求直线系与圆的割线中点的轨迹呢直线y=kx与圆x^2+y^2-6 2020-07-31 …
如图甲所示,弯曲部分AB和CD是两个半径都为0.3m的14圆弧轨道,中间的BC段是竖直的薄壁细圆管 2020-07-31 …
如图所示,间距为L、电阻不计的足够长的双斜面型平行导轨,左导轨光滑,右导轨粗糙,左、右导轨分别与水平 2020-12-09 …