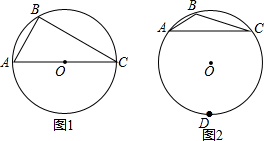
△ABC是O的内接三角形，BC=3．（1）如图1，若AC是O的直径，∠BAC=60°，延长BA到点D，使得DA=12BA，过点D作直线l⊥BD，垂足为点D，请将图形补充完整，判断直线l和O的位置关系并说明理由．（2

Question

△ABC是 O的内接三角形，BC=√(3)．
（1）如图1，若AC是 O的直径，∠BAC=60°，延长BA到点D，使得DA=(1)/(2)BA，过点D作直线l⊥BD，垂足为点D，请将图形补充完整，判断直线l和 O的位置关系并说明理由．
（2）如图2，∠B=120°，点D是优弧

AC

的中点，DE∥BC交BA延长线于点E，BE=2，请将图形补充完整并求AB的值．

Answer 1

（1）图形如图所示，直线l与 O相切．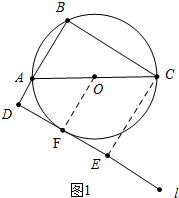
理由：作OF⊥l于F，CE⊥l于E，
∵AC是直径，
∴∠ABC=90°，
∵DE∥BC，
∴∠ABC+∠BDE=180°，
∴∠BDE=90°，
∴BD⊥DE，
∴AD∥OF∥CE，
∵AO=OC，
∴DF=FE，
∴OF=(1)/(2)（AD+CE），设AD=a，则AB=2AD=2a，
∵∠ABC=∠BDE=∠CED=90°，
∴四边形BDEC是矩形，
∴CE=BD=3a，
∴OF=2a，
∵在RT△ABC中，∠ABC=90°，∠ACB=30°，AB=2a，
∴AC=4a，
∴OF=OA，
∴直线l是 O切线．
（2）图形如图2所示，连接AD，BD，CD．
∵

AD

=

CD

，∠ABC=120°，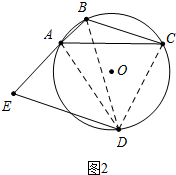
∴∠EBD=∠CBD=60°，
∵DE∥CB，
∴∠ABC+∠E=180°，
∴∠E=60°，
∴△BED是等边三角形，
∴∠EDB=60°，ED=DB，
∵∠ACD=∠ABD=60°，∠DAC=∠CBD=60°，
∴△ACD是等边三角形，
∴∠ADC=60°，DA=DC，
∴∠EDB=∠ADC，
∴∠EDA=∠BDC，
在△EDA和△BDC中，

ED=BD

∠ADE=∠BDC

DA=DC

，
∴△EDA≌△BDC，
∴AE=BC=√(3)，
∵BE=2，
∴AB=BE-AE=2-√(3)．