早教吧作业答案频道 -->数学-->
如图,若四边形ABCD是半径为1的⊙O的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为()A、(2π-2)cm2B、(2π-1)cm2C、(π-2)cm2D、
题目详情
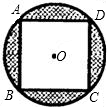 如图,若四边形ABCD是半径为1的⊙O的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为( )
如图,若四边形ABCD是半径为1的⊙O的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为( )| A、(2π-2)cm 2 | B、(2π-1)cm 2 | C、(π-2)cm 2 | D、(π-1)cm 2 |
▼优质解答
答案和解析
分析:
阴影部分的面积等于圆的面积减去正方形的面积,求出圆内接正方形的边长,即可求解.
连接AO,DO,∵ABCD是正方形,∴∠AOD=90°,AD=AO2+DO2=2,圆内接正方形的边长为2,所以阴影部分的面积=(π-2)cm2.故选C.
点评:
本题利用了圆内接正方形的边长与圆的半径的关系求解.
分析:
阴影部分的面积等于圆的面积减去正方形的面积,求出圆内接正方形的边长,即可求解.
连接AO,DO,∵ABCD是正方形,∴∠AOD=90°,AD=AO2+DO2=2,圆内接正方形的边长为2,所以阴影部分的面积=(π-2)cm2.故选C.
点评:
本题利用了圆内接正方形的边长与圆的半径的关系求解.
看了 如图,若四边形ABCD是半径...的网友还看了以下:
四个半径为R的球两两相切,在四球形成的间隙中放入一个半径为r的球使之与另外四球均相切,求R与r关系 2020-04-27 …
在四面体ABCD中,AD=2倍根号3,角BAC=60°角BAD=角CAD=45°.若过D与平面AB 2020-05-14 …
在平面几何里,我们知道,正三角形的外接圆和内切圆的半径之比是2:1。拓展到空间,研究正四面体(四个 2020-07-03 …
三角形的面积,a,b,c为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为 2020-07-23 …
设三角形ABC的三边长分别是a,b,c,三角形ABC的面积为S,内切圆的半径r=2S/a+b+c, 2020-07-31 …
(2014•池州二模)已知正四面体ABCD的棱长为4,设正四面体内切球半径为r,外接球半径为R,M 2020-07-31 …
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r=2Sa+b+c,类比 2020-07-31 …
(1)若三角形的内切圆半径为r,三边的长分别为a,b,c,则三角形的面积S=12r(a+b+c), 2020-08-01 …
平面上若一个三角形的周长为L,其内切圆的半径为R,则该三角形的面积S=12LR,类比到空间,若一个 2020-08-01 …
如图,在正三角形ABC中,内切圆半径外接圆半径=ODOA=ODAD-OD=ODAD1-ODAD,而O 2020-12-25 …