早教吧作业答案频道 -->数学-->
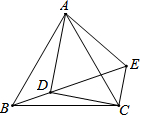
如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.(1)求证:AD=DE;(2)求∠DCE的度数;(3)若BD=1,求AD,CD的长.
题目详情
如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.

(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
▼优质解答
答案和解析
(1)证明:∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE,
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°-∠ADC-∠AEC-∠DAE=90°,
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC-∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中,DC=
=
=
.
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE,
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°-∠ADC-∠AEC-∠DAE=90°,
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC-∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中,DC=
| DE2-CE2 |
| 22-12 |
| 3 |
看了 如图,在等边△ABC中,点D...的网友还看了以下:
如图,D是等腰Rt△ABC的直角边BC上一点,AD的垂直平分线EF分别交AB,AC于点E,F,BC 2020-04-26 …
已知a大于0,b大于0,a+b=1,求证(a+1/a)(b+1/b)大于或等于25/4.解法里面有 2020-05-15 …
在直角三角形ABC中,角C=90度,斜边AB上的高CD=a,面积S为整数,且a,S满足条件:(S- 2020-05-16 …
已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三 2020-06-27 …
一已知数列{an}满足a1=1 a2=2 a(n+2)=(an+a(n+1))/21.令bn=a( 2020-06-27 …
1.设abcd是四个整数,且使m=(ab+cd)^2-1/4(a^2+b^2-c^2-d^2)^2 2020-07-09 …
1)在三角形ABC中,其面积为1/4(a^2+b^2-c^2),则角C=?2)已知:a,b,c分别 2020-07-30 …
初中三角函数:为什么sinA=cosB呢?还有一个问题是解直角三角形的:有3个角,3条边,其中直角是 2020-11-11 …
(2014•荆门模拟)已知函数f(x)=cos2x+3sinxcosx+2sinxcos(x+π6) 2020-11-12 …
在三角形ABC中,a,b,c分别是角ABC的对边长,已知根号2*sinA=根号(3*cosA)(1) 2020-12-25 …