早教吧作业答案频道 -->数学-->
如图,AB=AC,AD=AE,则:①△ABD≌△ACE;②△BOE≌△COD;③点O在∠BAC的平分线上.以上结论()A、都正确B、都不正确C、只有一个正确D、只有一个
题目详情
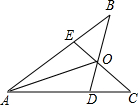 如图,AB=AC,AD=AE,则:①△ABD≌△ACE;②△BOE≌△COD;③点O在∠BAC的平分线上.以上结论( )
如图,AB=AC,AD=AE,则:①△ABD≌△ACE;②△BOE≌△COD;③点O在∠BAC的平分线上.以上结论( )| A、都正确 |
| B、都不正确 |
| C、只有一个正确 |
| D、只有一个不正确 |
▼优质解答
答案和解析
考点:
全等三角形的判定与性质
专题:
分析:
根据SAS推出△ABD≌△ACE,根据全等三角形的性质得出∠B=∠C,求出BE=CD,根据AAS推出△BOE≌△COD,根据全等得出OE=OD,根据SSS推出△AEO≌△ADO,根据全等三角形的性质得出∠BAO=∠CAO,即可得出选项.
在△ABD和△ACE中,AB=AC∠BAD=∠CAEAD=AE,∴△ABD≌△ACE(SAS),∴∠B=∠C,∵AB=AC,AE=AD,∴BE=CD,在△BOE和△COD中,∠BOE=∠COD∠B=∠CBE=CD,∴△BOE≌△COD(AAS),∴OE=OD,在△AEO和△ADO中,OE=ODAE=ADAO=AO,∴△AEO≌△ADO(SSS),∴∠BAO=∠CAO,∴点O在∠BAC的平分线上,∴①②③都正确,故选A.
点评:
本题考查了全等三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力,注意:全等三角形的判定定理是SAS,ASA,AAS,SSS,全等三角形的对应角相等,对应边相等.
考点:
全等三角形的判定与性质
专题:
分析:
根据SAS推出△ABD≌△ACE,根据全等三角形的性质得出∠B=∠C,求出BE=CD,根据AAS推出△BOE≌△COD,根据全等得出OE=OD,根据SSS推出△AEO≌△ADO,根据全等三角形的性质得出∠BAO=∠CAO,即可得出选项.
在△ABD和△ACE中,AB=AC∠BAD=∠CAEAD=AE,∴△ABD≌△ACE(SAS),∴∠B=∠C,∵AB=AC,AE=AD,∴BE=CD,在△BOE和△COD中,∠BOE=∠COD∠B=∠CBE=CD,∴△BOE≌△COD(AAS),∴OE=OD,在△AEO和△ADO中,OE=ODAE=ADAO=AO,∴△AEO≌△ADO(SSS),∴∠BAO=∠CAO,∴点O在∠BAC的平分线上,∴①②③都正确,故选A.
点评:
本题考查了全等三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力,注意:全等三角形的判定定理是SAS,ASA,AAS,SSS,全等三角形的对应角相等,对应边相等.
看了 如图,AB=AC,AD=AE...的网友还看了以下:
如图所示,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧, 2020-06-05 …
全等三角形的综合运用`这题怎么做`急以知三角行ABC中`角BAC=90`AB=AC,AE是过A的一 2020-06-07 …
如图1所示,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在A 2020-06-20 …
设矩阵A,B满足A=E(1,3)E(5(-2))BE(3,2(1/2)),则有A.B=E(1,3) 2020-06-28 …
一道↖(^ω^)↗↖(^ω^)↗↖(^ω^)↗在△ABC中,∠BAC=90°,AB=AC,AE是过 2020-07-03 …
求含元音字母且发元音的开音和闭音比如:A|ei|就是含有A且发|ei|的音的单词越多越好如:lat 2020-07-14 …
如图1所示,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在AE的异侧 2020-07-22 …
如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD 2020-11-02 …
如图1,△ABC中,角BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥ 2020-11-02 …
在正方形ABcD中,点P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,连接AE,过 2020-11-02 …