早教吧作业答案频道 -->数学-->
已知函数f(x)=|lnx|,g(x)=0,0<x≤1|x2-4|-2,x>1,则方程|f(x)+g(x)|=1实根的个数为
题目详情
已知函数f(x)=|lnx|,g(x)=
,则方程|f(x)+g(x)|=1实根的个数为___.
| |
|
▼优质解答
答案和解析
由|f(x)+g(x)|=1可得g(x)=-f(x)±1.
g(x)与h(x)=-f(x)+1的图象如图所示,图象有2个交点
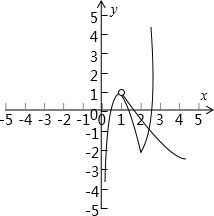
g(x)与φ(x)=-f(x)-1的图象如图所示,图象有两个交点;
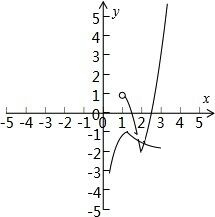
所以方程|f(x)+g(x)|=1实根的个数为4.
故答案为:4.
g(x)与h(x)=-f(x)+1的图象如图所示,图象有2个交点

g(x)与φ(x)=-f(x)-1的图象如图所示,图象有两个交点;

所以方程|f(x)+g(x)|=1实根的个数为4.
故答案为:4.
看了 已知函数f(x)=|lnx|...的网友还看了以下:
高分求解一道三角函数与导数综合题求证f(x)=sinx/(cosx的三次方根)-x在(0,90度) 2020-05-13 …
已知sinx,cosx为方程4x^2-4mx+2m-1=0的两个实根,x∈(-π/2,0)求m、x 2020-05-15 …
1.方程 x2│x│-5x│x│+2x=0的实根个数为____个.2.已知关于x的方程x^4+kx 2020-05-16 …
已知实系数二次函数f(x)与g(x)满足3f(x)+g(x)=0和f(x)-g(x)=0都有双重实 2020-06-22 …
问:若方程x²+x+a=0至少有一根为非负实数,求实数a的取值范围.书本上的解是这样的:若方程x² 2020-07-30 …
设m∈R,命题“若m≤0,则方程x2+x-m=0有实根”的逆否命题是()A.若方程x2+x-m=0 2020-07-30 …
若集合A={a|x^2-2x+a=0有实数根,B={ax^2-x+1=0}没有实数根,求A∩B若集 2020-08-01 …
a²(x²-x+1)-a(x²-1)=(a²-1)x(a≠0且a≠1)k取何值时?关于x的方程x²- 2020-11-20 …
若方程x^2+x+a=0至少有一根为非负实数,求实数a的取值范围.《王后雄》上给出的参考答案如下:若 2020-12-07 …
命题“若方程x^2+x-m=0"无实数根,则m小于等于0判断真假答x^2+x-m=0"命题“若方程x 2020-12-13 …