定义在R上的函数f(x)满足：如果对任意x1，x2∈R，都有f()≤[f(x1)＋f(x2)]，则称函数f(x)是R上的下凸函数．已知二次函数f(x)＝ax2＋x(a∈R，a≠0)．(1)求证：当a

Question

定义在R上的函数 f (x)满足：如果对任意x ₁ ，x ₂ ∈R，都有 f (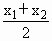 )≤ 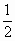[ f (x ₁ )＋ f (x ₂ )]，则称函数 f (x)是R上的下凸函数．

已知二次函数 f (x)＝ax ² ＋x(a∈R，a≠0)．

(1)求证：当a＞0时，函数 f (x)是下凸函数．

(2)如果x∈[0，1]时，| f (x)|≤1都成立，试求实数a的范围．

Answer 1

答案：
解析：
　　(1)对任意x＞0，∴[f(x)＋f(x)]－2f([()]＝x≥0． 　　∴f(≤[f]．∴函数f(x)是凹函数；(5分) 　　(2)由|f(x)|≤1－1≤f(x)≤1－1≤＋x≤1．(*) 　　当x＝0时，∈R；当x∈(0，1]时，(*)即 　　即∵x∈(0，1]，∴≥1．∴当＝1时，－(＋)－取得最大值是－2；当＝1时，(－)－取得最小值是0． 　　∴－2≤≤0，结合≠0，得－2≤＜0．综上，的范围是[－2，0)．(12分)