如图所示，已知PA⊥矩形ABCD所在平面，M，N分别是AB，PC的中点.(1)求证：MN∥平面PAD；(2)求证：MN⊥CD.(3)若∠PDA=45°求证：MN⊥平面PCD.

Question

如图所示，已知PA⊥矩形ABCD所在平面，M，N分别是AB，PC的中点.

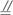
(1)求证：MN∥平面PAD；(2)求证：MN⊥CD.

(3)若∠PDA=45° 求证：MN⊥平面PCD.

Answer 1

【探究】 (1)要证明MN∥平面PAD，须证MN平行于平面PAD内某一条直线.注意到M，N分别为AB，PC的中点，可取PD的中点E，从而只须证明MN∥AE即可，证明如下：

证明：取PD的中点E，

连结AE、EN.

则EN CD AB AM，

故AMNE为平行四边形，∴MN∥AE.

∵AE 平面PAD，MN 平面PAD，∴MN∥平面PAD.

(2)要证MN⊥CD，可证MN⊥AB.

由问(1)知，需证AE⊥AB.

∵PA⊥平面ABCD.∴PA⊥AB，又AD⊥AB，

∴AB⊥平面PAD，∴AB⊥AE，即AB⊥MN.

又CD∥AB，∴MN⊥CD.

(3)由问(2)知，MN⊥CD，即AE⊥CD，再证AE⊥PD即可.

∵PA⊥平面ABCD，∴PA⊥AD.

又∠PDA=45° E为PD的中点.

∴AE⊥PD 即MN⊥PD.

又MN⊥CD.∴MN⊥平面PCD.

【规律总结】 本题是涉及线面垂直、线面平行、线线垂直诸知识点的一道综合题.题(1)的关键是选取PD的中点E，所作的辅助线使问题处理方向明朗化.线线垂直←线面垂直←线线垂直是转化规律.