如图，边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合，△EFG以每秒1个单位长度的速度沿BC向右匀速运动（保持FG⊥BC），当点E运动到CD边上时△EFG停止运动，设△EFG的

Question

如图，边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合，△EFG以每秒1个单位长度的速度沿BC向右匀速运动（保持FG⊥BC），当点E运动到CD边上时△EFG停止运动，设△EFG的运动时间为t秒，△EFG与正方形ABCD重叠部分的面积为S，则S关于t的函数大致图象为（　　）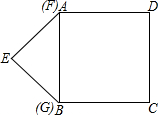

A.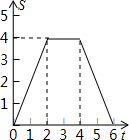

B.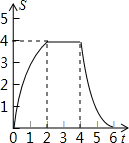

C.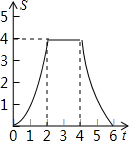

D.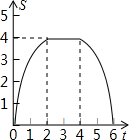

Answer 1

由题意可得，
FE=GE，AB=FG=4，∠FEG=90°，
则FE=GE=2√(2)，点E到FG的距离为2，
当点E从开始到点E到边BC上的过程中，S=(4×2)/(2)-(2(2-t)•(2-t))/(2)=-t²+4t（0≤t≤2），
当点E从BC边上到边FG与DC重合时，S=(4×2)/(2)=4（2≤t≤4），
当边FG与DC重合到点E到边DC的过程中，S=(2[2-(t-4)]×[2-(t-4)])/(2)=（6-t）²（4≤t≤6），
由上可得，选项B中函数图象符合要求，
故选B．