早教吧作业答案频道 -->数学-->
如图,已知H为锐角△ABC的垂心,D是使四边形AHCD为平行四边形的一点,过BC的中点M作AB的垂线,垂足为N,K为MN的中点,过点A作BD的平行线交MN于点G,若A,K,M,C四点共圆.求证:直线BK平分
题目详情
如图,已知H为锐角△ABC的垂心,D是使四边形AHCD为平行四边形的一点,过BC的中点M作AB的垂线,垂足为N,K为MN的中点,过点A作BD的平行线交MN于点G,若A,K,M,C四点共圆.求证:直线BK平分线段CG.
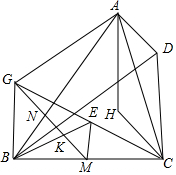

▼优质解答
答案和解析
证明:如图,
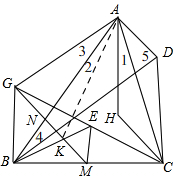
设BK交CG于E,连接AG,AK,
∵A,K,M,C四点共圆,
∴∠ACB=∠AKG(外角等于内对角),
∵H是△ABC的垂心,
∴AH⊥BC,CH⊥AB,
∵四边形AHCD是平行四边形,
∴CH∥AD,AH∥CD,
∴CD⊥BC,AD⊥AB,
∴∠BCD=∠BAD=90°,
∴∠BAD+∠BCD=180°,
∴点A,B,C,D四点共圆,
∴∠5=∠ACB=∠AKG,
∵AH⊥BC,
MN⊥AB,AD⊥AB,
∴∠1=∠2=∠4,
∵AG∥BD,
∴∠3=∠4=∠2,
在△ANG和△ANK中,
,
∴△ANG≌△ANK,
∴GN=KN=MK,
∴MK=
KG,
∵直线BKE截得△GMC,
由梅涅劳定理得:
•
•
=1,
∵点M是CB中点,
∴CB=2BM,
∴GE=EC,
∴直线BK平分线段CG.

设BK交CG于E,连接AG,AK,
∵A,K,M,C四点共圆,
∴∠ACB=∠AKG(外角等于内对角),
∵H是△ABC的垂心,
∴AH⊥BC,CH⊥AB,
∵四边形AHCD是平行四边形,
∴CH∥AD,AH∥CD,
∴CD⊥BC,AD⊥AB,
∴∠BCD=∠BAD=90°,
∴∠BAD+∠BCD=180°,
∴点A,B,C,D四点共圆,
∴∠5=∠ACB=∠AKG,
∵AH⊥BC,
MN⊥AB,AD⊥AB,
∴∠1=∠2=∠4,
∵AG∥BD,
∴∠3=∠4=∠2,
在△ANG和△ANK中,
|
∴△ANG≌△ANK,
∴GN=KN=MK,
∴MK=
| 1 |
| 2 |
∵直线BKE截得△GMC,
由梅涅劳定理得:
| GE |
| EC |
| CB |
| BM |
| MK |
| KG |
∵点M是CB中点,
∴CB=2BM,
∴GE=EC,
∴直线BK平分线段CG.
看了 如图,已知H为锐角△ABC的...的网友还看了以下:
如图在三角形ABC中,BC=12∠BAC=100度AB的垂直平分线叫BC边于点E,AC的垂直平分线 2020-06-06 …
初中平面几何谁帮我解了?任意一个直角三角型,M为斜边中点,P、Q两点分别为两直角边上任意两点,PM 2020-06-27 …
一道28题,请求擅长数学的人士解答,此题为初三学生的题如图所示,直线PD为三角形ABC一边BC的垂 2020-07-17 …
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.已知:如图,在△AB 2020-07-20 …
直角三角形斜边上中线与两直角边中点的连线的关系是1,相等2,相等且互相垂直3,相等且互相平分4,相 2020-07-21 …
如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,A 2020-07-27 …
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,角BCD=60度,AB=2AD,PD垂直平 2020-07-31 …
在下列四个命题中,假命题为()A.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直 2020-08-02 …
“一个三角形的三条边的垂直平分线的交点是这个三角形的外心”,这个句子的主干是()A.三角形是外心B. 2020-11-17 …
直角三角形斜边上的中线与连结两直角边中点的线段的关系是()A.相等且平分B.相等且垂直C.垂直平分D 2021-01-22 …