如图，锐角三角形ABC内接于半径为R的O，H是三角形ABC的垂心，AO的延长线与BC交于点M，若OH⊥AO，BC=10，OA=6，则OM的长=．

Question

如图，锐角三角形ABC内接于半径为R的 O，H是三角形ABC的垂心，AO的延长线与BC交于点M，若OH⊥AO，BC=10，OA=6，则OM的长=___．

Answer 1

如图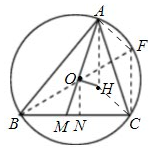，连接BO并延长交圆于F，连接CF，AH，连接AF，CH，过点O作ON⊥BC于N，
∵BF是 O的直径，
∴∠BCF=∠BAF=90°，
∴ON∥FC，
∵OB=OF，
∴ON是△BCF的中位线，
∴CF=2ON．
∴BN=CN=(1)/(2)BC=5，
在Rt△OBN中，OB=OA=6，BN=5，
∴ON=√(OB2-BN2)=√(11)，
∴CF=2ON=2√(11)，
∵H是△ABC的垂心，
∴AH⊥BC，
∵CF⊥BC，
∴AH∥CF，
同理可得：CH∥AF，
∴四边形AHCF是平行四边形，
∴AH=CF=2√(11)
∵H是△ABC的垂心，
∴AH⊥BC，
∵ON⊥BC，
∴AH∥ON，
∴∠OAH=∠NOM，
∵OH⊥AM，
∴∠AOH=∠ONM=90°，
∴△AOH∽△ONM，
∴(AH)/(OM)=(AO)/(ON)，
∴(2√(11))/(OM)=(6)/(√(11))，
∴OM=(11)/(3)．
故答案为(11)/(3)．