如图1，在△APE中，∠PAE=90°，PO是△APE的角平分线，以O为圆心，OA为半径作圆交AE于点G．（1）求证：直线PE是O的切线；（2）在图2中，设PE与O相切于点H，连结AH交PO于点D，已知PA=6，tan∠EAH=

Question

如图1，在△APE中，∠PAE=90°，PO是△APE的角平分线，以O为圆心，OA为半径作圆交AE于点G．

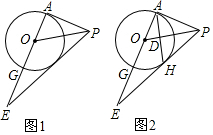
（1）求证：直线PE是 O的切线；
（2）在图2中，设PE与 O相切于点H，连结AH交PO于点D，已知PA=6，tan∠EAH=(2)/(3)．
①求 O的半径；
②求EH的长．

Answer 1

证明：（1）如图1，

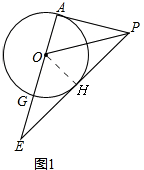
作OH⊥PE，
∴∠OHP=90°，
∵∠PAE=90，
∴∠OHP=∠OAP，
∵PO是∠APE的角平分线，
∴∠APO=∠EPO，
在△PAO和△PHO中，

∠OHP=∠OAP

∠OPH=∠OPA

OP=OP

，
∴△PAO≌△PHO，
∴OH=OA，
∵OA是 O的半径，
∴OH是 O的半径，
∴直线PE是 O的切线；
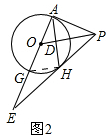（2）①如图2，∵∠PAO=90°，
∴PA切 O于A，
∵PE与 O相切于点H，
∴PA=PH=6，
∵PO是△APE的角平分线，
∴PO⊥AH，
∴∠APO+∠PAH=90°，
∵∠EAH+∠PAH=90°，
∴∠APO=∠EAH，
∵tan∠EAH=(2)/(3)．
∴tan∠APO=(2)/(3)．
在Rt△APO中，AP=6，tan∠APO=(OA)/(AP)=(2)/(3)，
∴OA=(2)/(3)AP=(2)/(3)×6=4，
②由①知，OA=4，
∴AG=2OA=8，
∵PE是 O的切线，
∴∠EHG=∠EAH，
∵∠HEG=∠AEH，
∴△EHG∽△EAH，
∴(EH)/(AE)=(GH)/(AH)=(EG)/(EH)，
在Rt△AHG中，tan∠EAH=(GH)/(AH)=(2)/(3)，
∴(EH)/(AE)=(EG)/(EH)=(2)/(3)，
∴EG=(2)/(3)EH，AE=(3)/(2)EH，
∵AE-EG=AG=8，
∴(3)/(2)EH-(2)/(3)EH=8，
∴EH=(48)/(5)．