早教吧作业答案频道 -->数学-->
已知正三角形ABC的边长为a,面积为s,内切圆的半径为r,则r=2s3a,类比这一结论可知:正四面体S-ABC的底面的面积为S,内切球的半径为R,体积为V,则R=.
题目详情
已知正三角形ABC的边长为a,面积为s,内切圆的半径为r,则r=
,类比这一结论可知:正四面体S-ABC的底面的面积为S,内切球的半径为R,体积为V,则R=___.
| 2s |
| 3a |
▼优质解答
答案和解析
设四面体的内切球的球心为O,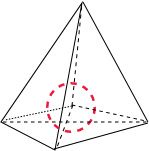
则球心O到四个面的距离都是R,
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
则四面体的体积为V=
•4SR
猜想:正四面体S-ABC的底面的面积为S,内切球的半径为R,体积为V,
则四面体ABCD的内切球半径R=
,
故答案:
.

则球心O到四个面的距离都是R,
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
则四面体的体积为V=
| 1 |
| 3 |
猜想:正四面体S-ABC的底面的面积为S,内切球的半径为R,体积为V,
则四面体ABCD的内切球半径R=
| 3V |
| 4S |
故答案:
| 3V |
| 4S |
看了 已知正三角形ABC的边长为a...的网友还看了以下:
边长为根号3等边三角形,高=?面积=?半径R=?边心距r=?O的半径为10,则其内接正四边形的边长 2020-04-13 …
solidworks倒圆角两个面圆角半径不一致.怎么操作命令.打个比方,2个相交的AB俩面倒圆角, 2020-05-17 …
一把雨伞,圆形伞面的半径为r,伞面边缘距地面的高度为h,以角速度ω旋转这把雨伞,问:(1)伞面边缘 2020-06-17 …
有一把雨伞圆形伞面的半径为r,伞边距离地面的高度为h,以角速度w旋转着把伞,问伞边缘上甩出去的水滴 2020-06-17 …
关于圆锥的侧面展开图的中心角求法问题如果圆锥的侧面积是全面积的3/4,求圆锥的侧面展开图的中心角. 2020-07-05 …
在平面直角坐标系中,以点(3,-5)为圆心,r为半径的圆上有且仅有两点到x轴所在直线的距离等于1, 2020-07-25 …
1扇形周长公式因为扇形周长=半径×2+弧长,若半径为r,直径为R,扇形所对的圆心角的度数为n°为啥 2020-07-26 …
在角速度的推导中dr为位移,r半径向量,dθk角速度dr=dθk×r的推导这样对不对dθk×r=d 2020-07-30 …
在平面三角形中,若ABC的三边长为a,b,c,其内切圆半径为r,有结论:ABC的面积S=12(a+ 2020-08-01 …
一公路的水平弯道半径为R,路面的外侧高出内侧,并与水平面夹角为θ。要使汽车通过该段路面时而不引起侧向 2020-12-27 …