已知f(x)是定义域为R的单调函数,且对任意的x∈R,都有f[f(x)-ex]=1,则函数g(x)=f(x)+f(-x)f(x)-f(-x)的图象大致是()A.B.C.D.
已知f(x)是定义域为R的单调函数,且对任意的x∈R,都有f[f(x)-ex]=1,则函数g(x)=
的图象大致是( )f(x)+f(-x) f(x)-f(-x)
A. 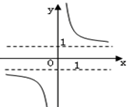
B. 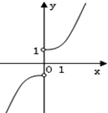
C. 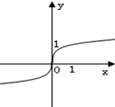
D. 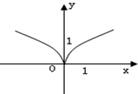
∴t+et=1,即 et=1-t,
∴t=0,即f(x)=ex.
∴函数g(x)=
| f(x)+f(-x) |
| f(x)-f(-x) |
| ex+e-x |
| ex-e-x |
| e2x+1 |
| e2x-1 |
| 2 |
| e2x-1 |
∴g(-x)=-g(x),故g(x)为奇函数,故它的图象关于原点对称.
当x>0时,g(x)为单调递减函数,故排除B.
∵
| 2 |
| e2x-1 |
故选:A.
已知函数f(x)=lnx,f′(x)是f(x)的导数,f′(x)的大致图象是()A.B.C.D. 2020-05-14 …
(2011•徐汇区三模)已知函数f(x)=|x|•(a-x),a∈R.(1)当a=4时,画出函数f 2020-06-08 …
(2014•碑林区一模)已知函数f(x)=(x-a)(x-b)(其中a>b),若f(x)的图象如图 2020-06-08 …
化简三角函数sin12*sin24*sin48*sin96=?函数f(x)=lnx-2/x的零点所 2020-06-13 …
给一点大致思路和过程,已知函数f(x)=x平方-2(1-m)x+2在区间(-无穷,4]是减函数,求 2020-06-27 …
已知函数f(x)={x^3,x≤1,log1/3x,(x>1),则函数y=f(1-x)的大致图像是 2020-07-27 …
已知函数f(x)=3sin(2x-π3)(x∈R).(1)用五点法画出函数f(x)在x∈[-5π6 2020-08-01 …
已知函数f(x)=x(|x|-2),x∈[-3,3].(1)判断函数f(x)的奇偶性,并说明理由; 2020-08-01 …
已知函数f(x)=xesin(x-π2)(e为自然对数的底数),当x∈[-π,π]时,y=f(x) 2020-08-02 …
(2013•绵阳模拟)已知函数f(x)=kax-a-x(a>0且a≠1)在R上是奇函数,且是增函数, 2020-11-12 …