已知二次函数h（x）=ax2+bx+c（c<4），其导函数y=h'（x）的图象如图所示，函数f（x）=8lnx+h（x）．（1）求a，b的值；（2）若函数f（x）在区间（m，m+12）上是单调增函数，求实数m的取值

Question

已知二次函数h（x）=ax²+bx+c（c<4），其导函数y=h'（x）的图象如图所示，函数f（x）=8lnx+h（x）．

（1）求a，b的值； 
（2）若函数f（x）在区间（m，m+(1)/(2)）上是单调增函数，求实数m的取值范围；
（3）若对任意k∈[-1，1]，x∈（0，8]，不等式（k+1）x≥f（x）恒成立，求实数c的取值范围．

Answer 1

（1）二次函数h（x）=ax²+bx+c的导数为：
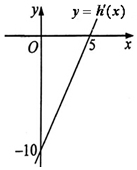
y=h′（x）=2ax+b，由导函数y=h′（x）的图象可知，
导函数y=h′（x）过点（5，0）和（0，-10），
代入h′（x）=2ax+b得：
b=-10，a=1；
（2）由（1）得：h（x）=x²-10x+c，h′（x）=2x-10，
f（x）=8lnx+h（x）=8lnx+x²-10x+c，
f′（x）=(8)/(x)+2x-10=(2(x-1)(x-4))/(x)，
当x变化时 

	（0，1）	1	（1，4）	4	（4，+∞）
f'（x）	+	0	-	0	+
f（x）	↗		↘		↗

所以函数f（x）的单调递增区间为（0，1）和（4，+∞）．
单调递减区间为（1，4），
若函数在（m，m+(1)/(2)）上是单调递增函数，则有

m≥0

m+(1)/(2)≤1

或者m≥4，解得0≤m≤(1)/(2)或m≥4；
故m的范围是：[0，(1)/(2)]∪[4，+∞）．
（3）若对任意k∈[-1，1]，x∈（0，8]，不等式（k+1）x≥f（x）恒成立，
即对k=-1时，x∈（0，8]，不等式c≤-x²-8lnx+10x恒成立，
设g（x）=-x²-8lnx+10x，x∈（0，8]，
则g′（x）=(-2(x-1)(x-4))/(x)，x∈（0，8]，
令g′（x）>0，解得：1<x<4，令g′（x）<0，解得：4<x≤8或0<x<1，
故g（x）在（0，1）递减，在（1，4）递增，在（4，8]递减，
故g（x）的最小值是g（1）或g（8），
而g（1）=9，g（8）=16-24ln3<4<9，c<4，
故c≤g（x）_min=g（8）=16-24ln3，
即c的取值范围是（-∞，16-24ln3]．