早教吧作业答案频道 -->数学-->
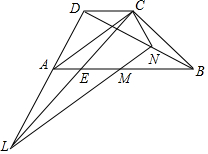
已知梯形ABCD中,对角线AC与腰BC相等,M是底边AB的中点,L是边DA延长线上一点连接LM并延长交对角线BD于N点.求证:∠ACL=∠BCN.
题目详情
已知梯形ABCD中,对角线AC与腰BC相等,M是底边AB的中点,L是边DA延长线上一点连接LM并延长交对角线BD于N点.求证:∠ACL=∠BCN.

▼优质解答
答案和解析
延长LM至G,使LM=MG,
∵AM=MB,LM=MG,
∴四边形ALBG是平行四边形,
∴AL=BG,AL∥GB,
∴
=
,
延长CN交AB于F,令LC与AB的交点为E,
∵AB是梯形ABCD的底边,
∴BF∥CD,
∴
=
,
由
=
,
得:
=
,
∴LC∥FG,
∴∠ELM=∠FGB,
∵AL∥GB,
∴∠LAE=∠GBF,∠ALM=∠BGM,
∴∠ALM-∠ELM=∠BGM-∠FGB,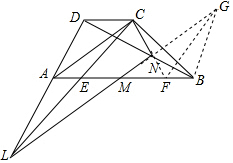
∴∠ALE=∠BGF,
在△ALE与△BGF中,
,
∴△ALE≌△BGF,
∴AE=BF,
∵AC=BC,
∴∠CAE=∠CBF,
在△ACE与△BCF中,
,
∴△ACG≌△BCF,
∴∠ACL=∠BCN.
∵AM=MB,LM=MG,
∴四边形ALBG是平行四边形,
∴AL=BG,AL∥GB,
∴
| LN |
| FN |
| DN |
| BN |
延长CN交AB于F,令LC与AB的交点为E,
∵AB是梯形ABCD的底边,
∴BF∥CD,
∴
| CN |
| FN |
| DN |
| BN |
由
| LN |
| FN |
| DN |
| BN |
得:
| LN |
| EN |
| DN |
| BN |
∴LC∥FG,
∴∠ELM=∠FGB,
∵AL∥GB,
∴∠LAE=∠GBF,∠ALM=∠BGM,
∴∠ALM-∠ELM=∠BGM-∠FGB,

∴∠ALE=∠BGF,
在△ALE与△BGF中,
|
∴△ALE≌△BGF,
∴AE=BF,
∵AC=BC,
∴∠CAE=∠CBF,
在△ACE与△BCF中,
|
∴△ACG≌△BCF,
∴∠ACL=∠BCN.
看了 已知梯形ABCD中,对角线A...的网友还看了以下:
四边形ABCD是正方形,点E在边BC上(不与端点B、C重合),点F在对角线AC上,且EF⊥AC,连 2020-06-15 …
如图1,将矩形ABCD绕点A顺时针旋转至矩形B点正好落在CD上的点E处,连结BE.(1)求证:∠B 2020-06-20 …
如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并 2020-07-10 …
如图所示,在两个等量正点电荷形成的电场中,O点是两电荷连线的中点,a、b是该线上的两点,c、d是两 2020-07-30 …
正方形里面画一个小正方形,连接对应的定点,取连线的中点,构成一个新的四边形,求证这个四边形是正方形 2020-07-30 …
将一个内角为120度的菱形纸片,沿着较长的对角线剪开,得到两张全等的三角形纸片,将这两张纸片摆放成 2020-08-02 …
下列说法中,正确的是()A.在成中心对称的图形中,连接对称点的线段不一定都经过对称中心B.在成中心 2020-08-02 …
已知等腰直角三角形ABC中,D为斜边BC上一点,过D点作DE⊥BC交AB于E,连接CE,F为CE中 2020-08-03 …
如图在等腰直角三角形ABC中,∠ACB=90°,点D为BC的中点,DE⊥AB,垂足为点E,过点B作B 2020-11-03 …
正方形abcd中,ab=6,点g是边bc的中点,连接ag,将三角形abg沿ag对折至三角形afg,( 2020-11-03 …