早教吧作业答案频道 -->物理-->
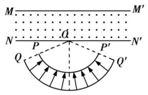
如图所示,PP′和QQ′是两个同心圆弧,圆心为O,O、P、Q和O、P′、Q′分别共线,∠NOQ=∠N′OQ′=30°,PP′和QQ′之间的区域内分布着辐射状的电场,UQP=25V.MM′和NN′为有界匀强磁场的边界
题目详情
如图所示,PP′和QQ′是两个同心圆弧,圆心为O,O、P、Q和O、P′、Q′分别共线,∠NOQ=∠N′OQ′=30°,PP′和QQ′之间的区域内分布着辐射状的电场,UQP=25V.MM′和NN′为有界匀强磁场的边界,MM′∥NN′,间距d=
m,磁场的磁感应强度大小为B=0.2T,方向如图所示.圆弧QQ′上均匀分布着质量为m=2×10-8kg、电荷量为q=4×10-4C的带正电粒子,它们被辐射状的电场由静止加速,之后进入磁场.不计粒子的重力以及粒子之间的相互作用.
(1)求粒子刚进入磁场时的速度大小.
(2)求粒子从上边界MM′飞出磁场需要的最短时间.
(3)若要保证所有粒子都能到达置于磁场下边界NN'上适当位置的收集板上,则磁场上边界MM′至少应向上平移多少?收集板至少多长?
| ||
| 4 |

(1)求粒子刚进入磁场时的速度大小.
(2)求粒子从上边界MM′飞出磁场需要的最短时间.
(3)若要保证所有粒子都能到达置于磁场下边界NN'上适当位置的收集板上,则磁场上边界MM′至少应向上平移多少?收集板至少多长?
▼优质解答
答案和解析
(1)粒子在电场中加速,
由动能定理得:qUQP=
mv2,
解得,粒子进入磁场的速度大小为v=1×103m/s;
(2)粒子从O点飞入磁场,在磁场中运动的速度大小不变,
则当轨迹圆弧所对应的弦长最短时,粒子在磁场中运动的路程最短,
即运动的时间最短,轨迹如图1所示.
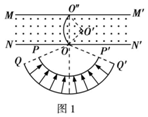
洛伦兹力提供向心力,由牛顿第二定律得:
qvB=m
,解得,轨道半径:r=0.25 m,
在△O'OO″中,O'O″=O'O=r=0.25 m,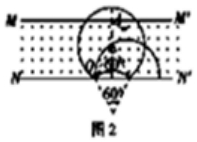
OO″=d=
m,可得∠O″O'O=90°
粒子在磁场中运动的周期:T=
,
则粒子从上边界飞出磁场需要的最短时间:t=
T=
×10-3s;
(3)若磁场足够大,由几何知识可知,沿O′P′方向射入的粒子在磁场中转过的圆心角最大,
能到达与NN′的最远距离为:d0=r(1+cos30°)处,
则上边界MM′至少应向上平移:△d=d0-d=
(2-2
+
)m,
沿QP方向和Q′P′方向射入的粒子在磁场中转过的圆心角分别为60°、300°,
由几何关系可知,从这两个方向射入磁场的粒子NN′方向的位移最小,
最小位移:smin=r,粒子垂直NN′方向进入磁场时沿NN′方向的位移最大,最大位移为2r,
则收集板的长度至少为:L=2r-r═r=0.25m;
答:(1)粒子刚进入磁场时的速度大小为1×103m/s.
(2)粒子从上边界MM′飞出磁场需要的最短时间为
×10-3s.
(3)磁场上边界MM′至少应向上平移
(2-2
+
)m,收集板长度至少为0.25m.
由动能定理得:qUQP=
| 1 |
| 2 |
解得,粒子进入磁场的速度大小为v=1×103m/s;
(2)粒子从O点飞入磁场,在磁场中运动的速度大小不变,
则当轨迹圆弧所对应的弦长最短时,粒子在磁场中运动的路程最短,
即运动的时间最短,轨迹如图1所示.

洛伦兹力提供向心力,由牛顿第二定律得:
qvB=m
| v2 |
| r |
在△O'OO″中,O'O″=O'O=r=0.25 m,

OO″=d=
| ||
| 4 |
粒子在磁场中运动的周期:T=
| 2πr |
| v |
则粒子从上边界飞出磁场需要的最短时间:t=
| 1 |
| 4 |
| π |
| 8 |
(3)若磁场足够大,由几何知识可知,沿O′P′方向射入的粒子在磁场中转过的圆心角最大,
能到达与NN′的最远距离为:d0=r(1+cos30°)处,
则上边界MM′至少应向上平移:△d=d0-d=
| 1 |
| 8 |
| 2 |
| 3 |
沿QP方向和Q′P′方向射入的粒子在磁场中转过的圆心角分别为60°、300°,
由几何关系可知,从这两个方向射入磁场的粒子NN′方向的位移最小,
最小位移:smin=r,粒子垂直NN′方向进入磁场时沿NN′方向的位移最大,最大位移为2r,
则收集板的长度至少为:L=2r-r═r=0.25m;
答:(1)粒子刚进入磁场时的速度大小为1×103m/s.
(2)粒子从上边界MM′飞出磁场需要的最短时间为
| π |
| 8 |
(3)磁场上边界MM′至少应向上平移
| 1 |
| 8 |
| 2 |
| 3 |
看了 如图所示,PP′和QQ′是两...的网友还看了以下:
在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始沿AB边向点B以1cm/s的 2020-04-27 …
在边长为4的正方形ABCD中,点P.Q在边AD,CD上,BF垂直PQ,垂足为F,且BF=AB.分别 2020-05-13 …
如图,在RT△ABC中,∠B=90°,AB=6,BC=8,点P从点A开始,沿AB边向点B以1cm/ 2020-05-16 …
在高200米的电视塔顶A处侧得地面有两个目标P,Q俯角分别为30度,45度,同时测得角PAQ也是4 2020-05-17 …
三角函数,急已知sinθ/2=-3/5,cosθ/2=4/5,则θ所在的象限?函数y=2sin(2 2020-05-22 …
三角形ABC是边长为3厘米的等边三角形,动点P,Q同时从A,B两点出发,他们的速度都是1厘米每秒, 2020-05-24 …
三角形ABC是边长为3厘米的等边三角形,动点P,Q同时从A,B两点出发,,分别沿AB,BC,方向匀 2020-05-24 …
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点p从点A开始沿AB边向点B以1 2020-06-15 …
离散数学中环算几条边K4有几边几面构造下面推理证明(1)前提:┑(p∧q),┑q∧r,┑r结论:┑ 2020-07-30 …
已知动直线x=t(t∈[pai/3,pai])与两函数f(x)=sinx,g(x)=√3·f(x-p 2020-12-23 …