早教吧作业答案频道 -->数学-->
对于椭圆=1,是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰好被直线=0平分?若存在,求出l的倾斜角的范围;若不存在,请说明理由.
题目详情
对于椭圆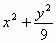 =1,是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰好被直线
=1,是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰好被直线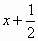 =0平分?若存在,求出l的倾斜角的范围;若不存在,请说明理由.
=0平分?若存在,求出l的倾斜角的范围;若不存在,请说明理由.
▼优质解答
答案和解析
答案:
解析:
设l的方程为y=kx+m,由得 (k2+9)x2+2kmx+m2-9=0, ∴Δ=4k2m2-4(k2+9)(m2-9)>0, 即m2-k2-9<0. 又, ∴m=.∴-(k2+9)<0. 解得k2>3,即k>或k<, ∴倾斜角又满足<α<或<α<, 即满足条件的直线l存在,其倾斜角的范围是(,)∪(,).
提示:
此类存在性问题的一般解题思路是假设存在,按题目条件,求出则说明存在;若推出矛盾结果,则说明不存在,可设出l的方程与椭圆方程组成方程组,利用韦达定理、中点坐标公式求解,同时要注意Δ>0的要求.
解析:
设l的方程为y=kx+m,由得 (k2+9)x2+2kmx+m2-9=0, ∴Δ=4k2m2-4(k2+9)(m2-9)>0, 即m2-k2-9<0. 又, ∴m=.∴-(k2+9)<0. 解得k2>3,即k>或k<, ∴倾斜角又满足<α<或<α<, 即满足条件的直线l存在,其倾斜角的范围是(,)∪(,).
提示:
此类存在性问题的一般解题思路是假设存在,按题目条件,求出则说明存在;若推出矛盾结果,则说明不存在,可设出l的方程与椭圆方程组成方程组,利用韦达定理、中点坐标公式求解,同时要注意Δ>0的要求.
看了 对于椭圆=1,是否存在直线l...的网友还看了以下:
设F1,F2分别为椭圆C:x2/a2+y2/b2=1(a>b>0),F1,F2为左右焦点,过F2的 2020-05-15 …
已知直线l经过点p(1/2,1)倾斜角a=π/6,在极坐标系下,圆c的极坐标方程为ρ=√2cos( 2020-07-22 …
关于圆·★已知圆C过P(1,1),且与圆(X+3)平方+(Y+3)平方=R平方关于直线X+Y+3= 2020-07-22 …
已知圆C在x轴上的截距为-1和3,在y轴上的一个截距为1.(1)求圆C的标准方程;(2)若过点(2 2020-07-30 …
已知椭圆C:x平方/a平方+y平方/b平方=1(a大于b大于0)的短轴长与焦距相等,且过定点(1, 2020-07-31 …
1.一个圆柱形容器的容积是一升,内装有一些液体,当容器倾斜到如下图所示的位置时,液体刚好不溢出.如 2020-07-31 …
已知直线l过A(-3,1),且倾斜角为45°已知直线L过点A(-3,1),且倾斜角为45°,直线L 2020-08-01 …
关于直线与椭圆的解析几何已知椭圆C:x2/2+y2/4=1,过椭圆上一点P(1,根号2)作倾斜角互 2020-08-01 …
设椭圆C:x^2/a^2+y^2/b^2=1(a>b>0)的右焦点为F,过F的直线l与椭圆C相交于 2020-08-01 …
已知A(1,1)是椭圆x^2/a^2+y^2/b^2(a>b>0)上一点F1,F2是椭圆的两焦点,且 2020-11-07 …