早教吧作业答案频道 -->数学-->
已知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,顶点A1在底面ABC上的射影O是△ABC的中心,AA1与AB的夹角为45°(1)求证:AA1⊥平面A1BC;(2)侧面BB1C1C是矩形;(3)求棱柱的侧面积.
题目详情
已知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,顶点A1在底面ABC上的射影O是△ABC的中心,AA1与AB的夹角为45°
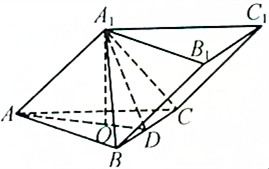
(1)求证:AA1⊥平面A1BC;
(2)侧面BB1C1C是矩形;
(3)求棱柱的侧面积.

(1)求证:AA1⊥平面A1BC;
(2)侧面BB1C1C是矩形;
(3)求棱柱的侧面积.
▼优质解答
答案和解析
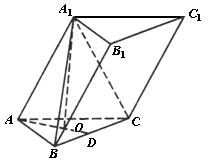 (1)如图,∵A1在底面ABC上的射影O为正△ABC的中心,
(1)如图,∵A1在底面ABC上的射影O为正△ABC的中心,
∴A1A=A1B=A1C.
又∵∠A1AB=45°,
∴∠A1BA═∠A1CA═∠A1AC═45°,
∴∠AA1B═∠AA1C═90°,即AA1⊥A1B,AA1⊥A1C,
又A1B∩A1C═A1,
∴AA1⊥平面A1BC.
(2)连AO并延长交BC于D,由条件知:AD⊥BC,AO为AA1在底面ABC的射影,
∴AA1⊥BC.
∵BB1∥AA1,
∴BB1⊥BC,
∴BCC1B1是矩形,
(3)在Rt△AA1B中,AA1=A1B=
AB,BC=2,
∴S AA1B1B=2S △AA1B=AA1•ABsin45°=2,S BCC1B1=2
,
∴S侧=2S AA1B1B+S BCC1B1=4+2
.
 (1)如图,∵A1在底面ABC上的射影O为正△ABC的中心,
(1)如图,∵A1在底面ABC上的射影O为正△ABC的中心,∴A1A=A1B=A1C.
又∵∠A1AB=45°,
∴∠A1BA═∠A1CA═∠A1AC═45°,
∴∠AA1B═∠AA1C═90°,即AA1⊥A1B,AA1⊥A1C,
又A1B∩A1C═A1,
∴AA1⊥平面A1BC.
(2)连AO并延长交BC于D,由条件知:AD⊥BC,AO为AA1在底面ABC的射影,
∴AA1⊥BC.
∵BB1∥AA1,
∴BB1⊥BC,
∴BCC1B1是矩形,
(3)在Rt△AA1B中,AA1=A1B=
| ||
| 2 |
∴S AA1B1B=2S △AA1B=AA1•ABsin45°=2,S BCC1B1=2
| 2 |
∴S侧=2S AA1B1B+S BCC1B1=4+2
| 2 |
看了 已知斜三棱柱ABC-A1B1...的网友还看了以下:
四棱锥P-ABCD的底面是正方形.在线等 速度~四棱锥P-ABCD的底面是正方形 PA⊥底面ABC 2020-05-16 …
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB 2020-07-09 …
(2014•天津)如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=2,AD=2,P 2020-07-29 …
如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB 2020-07-31 …
垂直关系1.在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E,F分别是AB,CD 2020-07-31 …
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB, 2020-10-31 …
(多u1u•济南一模)如图:已知正方体ABCD-A1B1C1D1,过BD1的平面分别交棱AA1和棱C 2020-10-31 …
(201人•文登市6模)在四棱锥P-AB我5中,AB∥我5,AB=125我=1,BP=B我=2,P我 2020-10-31 …
已知侧棱垂直于底面的四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1= 2020-11-02 …
已知四棱锥P-ABCD中,底面ABCD为正方形,PC⊥平面ABCD,AB=1,PC=2,E为侧棱PC 2020-12-23 …