三棱柱ABC-A1B1C1中，它的体积是153，底面△ABC中，∠BAC=90°，AB=4，AC=3，B1在底面的射影是D，且D为BC的中点．（1）求侧棱BB1与底面ABC所成角的大小；（2）求异面直线B1D与CA1所成角的大小．

Question

三棱柱ABC-A₁B₁C₁中，它的体积是15√(3)，底面△ABC中，∠BAC=90°，AB=4，
AC=3，B₁在底面的射影是D，且D为BC的中点．

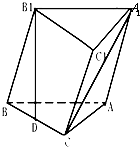
（1）求侧棱BB₁与底面ABC所成角的大小；
（2）求异面直线B₁D与CA₁所成角的大小．

Answer 1

（1）依题意，B₁D⊥面ABC，
∠B₁BD就是侧棱BB₁与底面ABC所成的角θ，
由VABC-A1B1C1=S△ABC•B1D=(1)/(2)×4×3×B1D=15√(3)，
则B1D=(5)/(2)√(3)，
由D为BC的中点，BC=√(42+32)=5，
即有BD=(5)/(2)，
由B1D=BDtanθ=(5)/(2)tanθ，即tanθ=√(3)，
∴θ=(π)/(3)，即侧棱BB₁与底面ABC所成角为(π)/(3)；
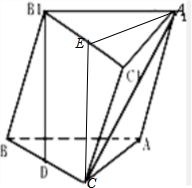
（2）取B₁C₁的中点E，连EC，A₁E，
则∠ECA₁（或其补角）为所求的异面直线所成角的大小，
B₁D⊥面ABC，B₁D‖CE，面ABC‖面A₁B₁C₁∴CE⊥面A₁B₁C₁，
∴CE⊥A₁E，tan∠A₁CE=(A1E)/(EC)=((5)/(2))/((5√(3))/(2))=(√(3))/(3)，
所求异面直线B₁D与CA₁所成角为(π)/(6)．