早教吧作业答案频道 -->数学-->
如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC,AB=AD=DE=2,EF=4,M是线段AE上的动点.(1)试确定点M的位置,使AC∥平面MDF,并说明理由;(2
题目详情
如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC,AB=AD=DE=2,EF=4,M是线段AE上的动点.
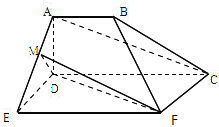
(1)试确定点M的位置,使AC∥平面MDF,并说明理由;
(2)在(1)的条件下,平面MDF将几何体ADE-BCF分成两部分,求空间几何体M-DEF与空间几何体ADM-BCF的体积之比.

(1)试确定点M的位置,使AC∥平面MDF,并说明理由;
(2)在(1)的条件下,平面MDF将几何体ADE-BCF分成两部分,求空间几何体M-DEF与空间几何体ADM-BCF的体积之比.
▼优质解答
答案和解析
(1)当M是线段AE的中点时,AC∥平面MDF,证明如下:(1分)
连结CE交DF于N,连结MN,由于M、N分别是AE、CE的中点,
所以MN∥AC,又MN在平面MDF内,(4分)
所以AC∥平面MDF (6分)
(2)将几何体ADE-BCF补成三棱柱ADE-B'CF,
三棱柱ADE-B'CF的体积为V=S△ADE•CD=
×2×2×4=8(8分)
则几何体ADE-BCF的体积:
VADE-BCF=V三棱柱ADE-ECF-VF-BB‘C=8-
×(
×2×2)×2=
(10分)
又三棱锥F-DEM的体积V三棱锥F-DEM=
×(
×2×4)×1=
,(11分)
∴空间几何体M-DEF与空间几何体ADM-BCF的体积之比为:
:(
-
)=
(12分)

连结CE交DF于N,连结MN,由于M、N分别是AE、CE的中点,
所以MN∥AC,又MN在平面MDF内,(4分)
所以AC∥平面MDF (6分)
(2)将几何体ADE-BCF补成三棱柱ADE-B'CF,
三棱柱ADE-B'CF的体积为V=S△ADE•CD=
| 1 |
| 2 |
则几何体ADE-BCF的体积:
VADE-BCF=V三棱柱ADE-ECF-VF-BB‘C=8-
| 1 |
| 3 |
| 1 |
| 2 |
| 20 |
| 3 |
又三棱锥F-DEM的体积V三棱锥F-DEM=
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
∴空间几何体M-DEF与空间几何体ADM-BCF的体积之比为:
| 4 |
| 3 |
| 20 |
| 3 |
| 4 |
| 3 |
| 1 |
| 4 |
看了 如图,空间几何体ADE-BC...的网友还看了以下:
正方体ABCD-A'B'C'D'中,点P在侧面BCC'B'及其边上运动,并且总是保持AP⊥BD', 2020-05-16 …
如图1,将一张对边平行的纸条沿ef折叠,点a,b分别落在a',b'处,线段fb'与ad交与点m.1 2020-06-02 …
如果a+√2ab+b=√2,且b是有理数,那么()a+根号(2)ab+b-根号2,且b是有理数,那 2020-06-14 …
给定双曲线x^2-y^2/2=1,过点B(1,1),是否能作直线m,是她与所给的双曲线教育两点Q1 2020-07-08 …
已知O、A、M、B为平面上四点,且OM=λOB+(1-λ)OA,λ∈(1,2),则()A.点M在线 2020-07-24 …
1.如图所示,已知线段AB=20cm,点M是线段AB中点,点C是线段AB延长线上的点,AC=3BC 2020-07-25 …
[说明]设有A,B,C,D四台主机,希望使A,B在同一物理网段,C,D在同一物理网段,并且每个网段除 2020-11-20 …
“归去来兮”一语全文两现,对其用意理解不当的一项是A.第一段首句开门见山,直抒胸臆,让人感觉他此志已 2020-12-03 …
如图1,点B在线段AC上的黄金分割点,且AB>BC.(1)设AC=2,①求AB的长;填空:设AB=x 2020-12-05 …
数据处理的三个阶段不包括()A.人工管理阶段B.计算机管理阶段C.文件系统管理阶段D.数据库系统管理 2020-12-25 …