早教吧作业答案频道 -->数学-->
如图,直线l1:y1=kx+2(k≠0)与直线l2:y2=4x-4交于点P(m,4),直线l1分别交x轴、y轴于点A、B,直线l2交x轴于点C.(1)求k、m的值;(2)写出使得不等式kx+2<4x-4成立的x的取值范围;(3)
题目详情
如图,直线l1:y1=kx+2(k≠0)与直线l2:y2=4x-4交于点P(m,4),直线l1分别交x轴、y轴于点A、B,直线l2交x轴于点C.
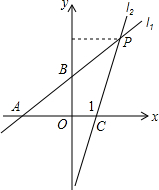
(1)求k、m的值;
(2)写出使得不等式kx+2<4x-4成立的x的取值范围;
(3)在直线l2上找点Q,使得S△QAC=S△BPC,求点Q的坐标.

(1)求k、m的值;
(2)写出使得不等式kx+2<4x-4成立的x的取值范围;
(3)在直线l2上找点Q,使得S△QAC=S△BPC,求点Q的坐标.
▼优质解答
答案和解析
(1)把P(m,4)代入y2=4x-4得4m-4=4,解得m=2,
所以P点坐标为(2,4),
把P(2,4)代入y1=kx+2得2k+2=4,解得k=1;
(2)当x>2时,kx+2<4x-4;
(3)当y=0时,x+2=0,解得x=-2,则A(-2,0);当x=0时,y1=x+2=2,则B(0,2),
当y=0时,4x-4=0,解得x=1,则C(1,0),
所以S△BPC=S△PAC-S△BAC=
×(1+2)×4-
×(1+2)×2=3,
设Q点坐标为(t,4t-4),
因为S△QAC=S△BPC=3,
所以
×(1+2)×|4t-4|=3,解得t=
或t=
,
所以Q点的坐标为(
,2)或(
,2).
所以P点坐标为(2,4),
把P(2,4)代入y1=kx+2得2k+2=4,解得k=1;
(2)当x>2时,kx+2<4x-4;
(3)当y=0时,x+2=0,解得x=-2,则A(-2,0);当x=0时,y1=x+2=2,则B(0,2),
当y=0时,4x-4=0,解得x=1,则C(1,0),
所以S△BPC=S△PAC-S△BAC=
| 1 |
| 2 |
| 1 |
| 2 |
设Q点坐标为(t,4t-4),
因为S△QAC=S△BPC=3,
所以
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以Q点的坐标为(
| 1 |
| 2 |
| 3 |
| 2 |
看了如图,直线l1:y1=kx+2...的网友还看了以下:
如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.(1)求证:△ADE∽△BE 2020-07-09 …
已知关于x的一元二次方程kx2-2(k+1)x+k-1=0有两个不相等的实数根x1,x2.(1)求 2020-07-16 …
(2014•山东模拟)已知函数f(x)=kx+2,x≤0lnx,x>0(k∈R),若函数y=|f( 2020-07-16 …
已知关于x.y的方程组x+2y=5k−2x−y=−k+4的解是一对异号的数.(1)求k的取值范围; 2020-07-30 …
下列各项中字音不正确的一项是:()A.裨(bì)益姓郝(hǎo)汲(jí)取B.吸(xī)取僭(ji 2020-11-07 …
如图,在Rt△ABC中,AC=3cm,BC=4cm,四边形CFDE为矩形,其中CF,CE在两直角边上 2020-11-30 …
如图,在Rt△ABC中,AC=3cm,BC=4cm,四边形CFDE为矩形,其中CF,CE在两直角边上 2020-11-30 …
设函数y=f(x)在(-∞,+∞)内有意义.对于给定的正数k,已知函数fk(x)=f(x),f(x) 2020-12-22 …
现有氧化铜和碳粉的混合物共mg,将它们隔绝空气加热,反应完全后冷却,得到残留固体.(1)写出可能发生 2020-12-24 …
对于直线l的倾斜角α与斜率k,下列说法错误的是()A.α的取值范围是[0°,180°)B.k的取值范 2021-02-04 …