早教吧作业答案频道 -->数学-->
如图(1),在矩形ABCD中,将矩形折叠,使点B落在AD(含端点)上,落点记为E,这时,折痕与边BC或边CD(含端点)交于点F,然后再展开铺平,则以点B、E、F为顶点的△BEF称为矩形ABCD的“折
题目详情
如图(1),在矩形ABCD中,将矩形折叠,使点B落在AD(含端点)上,落点记为E,这时,折痕与边BC或边CD(含端点)交于点F,然后再展开铺平,则以点B、E、F为顶点的△BEF称为矩形ABCD的“折痕三角形”.
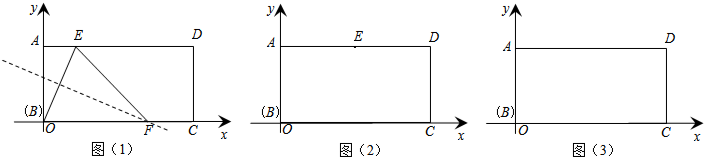
(1)如图(2),在矩形ABCD中,AB=2,BC=4,当它的“折痕△BEF”的顶点位于边AD的中点时,画出“折痕△BEF”,并求出点F的坐标;
(2)如图(3),在矩形ABCD中,AB=2,BC=4,该矩形是否存在面积最大的“折痕△BEF”?若存在,求出点E的坐标,若不存在,说明理由.

(1)如图(2),在矩形ABCD中,AB=2,BC=4,当它的“折痕△BEF”的顶点位于边AD的中点时,画出“折痕△BEF”,并求出点F的坐标;
(2)如图(3),在矩形ABCD中,AB=2,BC=4,该矩形是否存在面积最大的“折痕△BEF”?若存在,求出点E的坐标,若不存在,说明理由.
▼优质解答
答案和解析
(1)折痕△BEF如图(2)中所示,
连接BE,画BE的中垂线交BC与点F,连接EF,△BEF是矩形ABCD的一个折痕三角形.
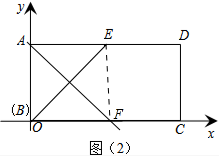
∵折痕垂直平分BE,AB=AE=2,
∴点A在BE的中垂线上,即折痕经过点A.
∴四边形ABFE为正方形.
∴BF=AB=2,
∴F(2,0).
(2)矩形ABCD存在面积最大的折痕三角形BEF,其面积为4,
理由如下:①当F在边BC上时,如图(3)中所示.
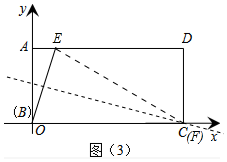
S△BEF≤
S矩形ABCD,即当F与C重合时,面积最大为4.
②当F在边CD上时,如图(4)中所示,
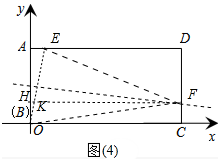
过F作FH∥BC交AB于点H,交BE于K.
∵S△EKF=
KF•AH≤
HF•AH=
S矩形AHFD,
S△BKF=
KF•BH≤
HF•BH=
S矩形BCFH,
∴S△BEF≤
S矩形ABCD=4.
即当F为CD中点时,△BEF面积最大为4.
下面求面积最大时,点E的坐标.
①当F与点C重合时,如图(3)所示.
由折叠可知CE=CB=4,
在Rt△CDE中,ED=
=2
.
∴AE=4-2
.
∴E(4-2
,2).
②当F在边DC的中点时,点E与点A重合,此时E(0,2).
综上所述,折痕△BEF的最大面积为4时,点E的坐标为E(0,2)或E(4-2
,2).
连接BE,画BE的中垂线交BC与点F,连接EF,△BEF是矩形ABCD的一个折痕三角形.

∵折痕垂直平分BE,AB=AE=2,
∴点A在BE的中垂线上,即折痕经过点A.
∴四边形ABFE为正方形.
∴BF=AB=2,
∴F(2,0).
(2)矩形ABCD存在面积最大的折痕三角形BEF,其面积为4,
理由如下:①当F在边BC上时,如图(3)中所示.

S△BEF≤
| 1 |
| 2 |
②当F在边CD上时,如图(4)中所示,

过F作FH∥BC交AB于点H,交BE于K.
∵S△EKF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S△BKF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BEF≤
| 1 |
| 2 |
即当F为CD中点时,△BEF面积最大为4.
下面求面积最大时,点E的坐标.
①当F与点C重合时,如图(3)所示.
由折叠可知CE=CB=4,
在Rt△CDE中,ED=
| CE2-CD2 |
| 3 |
∴AE=4-2
| 3 |
∴E(4-2
| 3 |
②当F在边DC的中点时,点E与点A重合,此时E(0,2).
综上所述,折痕△BEF的最大面积为4时,点E的坐标为E(0,2)或E(4-2
| 3 |
看了如图(1),在矩形ABCD中,...的网友还看了以下:
“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表达式为S=a+b2-1,孔明只记得公式中 2020-04-09 …
图中3个长方形(边a,b)2个正方形(边b),1个正方形(a),验证一个多项式的因式分解拼成一个大 2020-05-16 …
阅读下列材料:问题:在平面直角坐标系xOy中,一张矩形纸片OBCD按图1所示放置.已知OB=10, 2020-06-14 …
“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表示式为S=a+b2-1,小明只记得公式中 2020-07-05 …
在平面直角坐标系中,一张矩形纸片OBCD按图1所示放置,已知OB=10,BC=6,将这张纸片折叠, 2020-07-21 …
阅读下列材料:问题:在平面直角坐标系中,一张矩形纸片OBCD按图1所示放置。已知OB=10,BC= 2020-07-22 …
已知集合A={(x,y)|x|+|y|=a,a>0}B={(x,y}||xy|+1=|x|+|y| 2020-07-30 …
在三角形ABC中,角A,B,C所对边分别为a,b,c且tanA=1/2.(1)求tanC值(2)若 2020-07-30 …
如图,在△OMN中,A,B分别是OM,ON中点,若OP=xOA+yOB(x,y∈R),且点P落在四 2020-07-31 …
如图(1),在矩形ABCD中,将矩形折叠,使点B落在AD(含端点)上,落点记为E,这时,折痕与边BC 2020-11-01 …