早教吧作业答案频道 -->数学-->
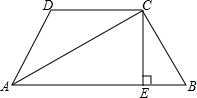
如图,已知在四边形ABCD中.∠B+∠D=180°,AC平分∠BAD,CE⊥AD,E为垂足.求证:AB+AD=2AE.
题目详情
如图,已知在四边形ABCD中.∠B+∠D=180°,AC平分∠BAD,CE⊥AD,E为垂足.求证:AB+AD=2AE.

▼优质解答
答案和解析
证明:如图,
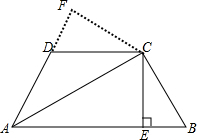
过C作CF⊥AD的延长线于点F,
∵AC平分∠BAD,
∴∠FAC=∠EAC,
∵CE⊥AB,CF⊥AD,
∴∠DFC=∠CEB=90°,
在△AFC和△AEC中,
,
∴△AFC≌△AEC,
∴AF=AE,CF=CE,
∵∠ADC+∠B=180°,
∴∠FDC=∠EBC,
在△FDC和△EBC中,
,
∴△FDC≌△EBC,
∴DF=EB,
∴AB+AD=AE+EB+AD=AE+DF+AD=AF+AE=2AE,
∴AB+AD=2AE.

过C作CF⊥AD的延长线于点F,
∵AC平分∠BAD,
∴∠FAC=∠EAC,
∵CE⊥AB,CF⊥AD,
∴∠DFC=∠CEB=90°,
在△AFC和△AEC中,
|
∴△AFC≌△AEC,
∴AF=AE,CF=CE,
∵∠ADC+∠B=180°,
∴∠FDC=∠EBC,
在△FDC和△EBC中,
|
∴△FDC≌△EBC,
∴DF=EB,
∴AB+AD=AE+EB+AD=AE+DF+AD=AF+AE=2AE,
∴AB+AD=2AE.
看了如图,已知在四边形ABCD中....的网友还看了以下:
高一必修二数学平面几何问题··求四点共线···如图,一直四边形ABCD中,AB‖CD,四条边AB,B 2020-03-30 …
已知EFGH分别是空间四边形ABCD四条边AB,BC,CD,DA的中点,求证四边形EFGH是平行四 2020-05-16 …
如图,ABCD是边长为1的正方形,E,F,G,H分别是四条边AB,BC,CD,DA的中点.计算图中 2020-05-16 …
如图,四边形ABCD内有一点P到四条边AB、BC、CD、DA的距离PE、PF、PM、PN都等于6厘 2020-05-23 …
四边形ABCD内有一点P到四条边AB.B四边形ABCD内有一点P到四条边AB.BC.CD.DA的距 2020-05-23 …
如图,四边形ABCD内有一点P到四条边AB、BC、CD、DA的距离PE、PF、PM、PN都等于6厘 2020-05-23 …
2题数学求证矩形1.E平行四边形ABCD的边AB的中点,并且EC=ED求证平行四边形ABCD为矩形 2020-07-13 …
如图,将四边形ABCD的四条边AB、CB、CD、AD分别延长两倍至点E、F、G、H,若四边形ABC 2020-07-20 …
如图,菱形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是它的四条边AB、BC、CD、DA 2020-12-25 …
如图,四边形EFGH为空间四边形ABCD的一个截面,四边形EFGH为平行四边形.(1)求证:AB∥平 2020-12-25 …