早教吧作业答案频道 -->数学-->
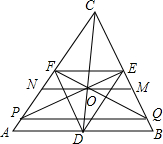
如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.
题目详情
如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.

▼优质解答
答案和解析
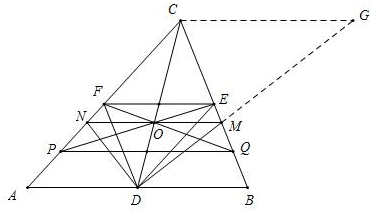
证明:如图:
∵DN平分∠ADC,
∴
=
,
同理
=
,
∵BD=AD,
∴
=
,
∴MN∥AB,
∴
=
=
,
∴ON=OM,
∵E、F分别是AC、BC的中点,
∴EF∥AB,EF=AD=BD,
∴EF∥MN,
∴
=
,
=
,
∴
=
,
∴PQ∥EF∥MN∥AB,
过点C作CG∥AB交DM的延长线于点G,如图,
∴∠CGD=∠GDB,
∵∠CDG=∠GDB,
∴∠CDG=∠CGD,
∴CD=CG,
∵
=
,
=
,
∴
+
=
+
=
=1,
又∵
=
,
=
∴
+
=
+
=
=1,
∵OM=ON,EF=BD,
∴CG=PQ,
∵CG=CD,
∴CD=PQ.

∵DN平分∠ADC,
∴
| CN |
| AN |
| CD |
| AD |
同理
| CM |
| BM |
| CD |
| BD |
∵BD=AD,
∴
| CN |
| AN |
| CM |
| BM |
∴MN∥AB,
∴
| ON |
| AD |
| CO |
| CD |
| OM |
| BD |
∴ON=OM,
∵E、F分别是AC、BC的中点,
∴EF∥AB,EF=AD=BD,
∴EF∥MN,
∴
| ON |
| EF |
| OP |
| PE |
| OM |
| EF |
| OQ |
| FQ |
∴
| PO |
| PE |
| QO |
| QF |
∴PQ∥EF∥MN∥AB,
过点C作CG∥AB交DM的延长线于点G,如图,
∴∠CGD=∠GDB,
∵∠CDG=∠GDB,
∴∠CDG=∠CGD,
∴CD=CG,
∵
| OM |
| CG |
| OD |
| CD |
| OM |
| BD |
| OC |
| CD |
∴
| OM |
| CG |
| OM |
| BD |
| OD |
| CD |
| OC |
| CD |
| CD |
| CD |
又∵
| ON |
| EF |
| PN |
| PF |
| ON |
| PQ |
| FN |
| FP |
∴
| ON |
| EF |
| ON |
| PQ |
| PN |
| PF |
| NF |
| PF |
| PF |
| PF |
∵OM=ON,EF=BD,
∴CG=PQ,
∵CG=CD,
∴CD=PQ.
看了如图,设D,E及F分别是△AB...的网友还看了以下:
如图所示,已知AD与BC相交于点E,角1=角2=角3,BD=CD,角ADB=90度,CH垂直AB于 2020-05-14 …
如何用调和点列证明牛顿线啊?牛顿线:四边形ABCD中,AB、CD交于点E,AD、BC交于点F,BD 2020-05-15 …
已知,在△ABC中,AB>AC,M为BC边上的中点,过M点的直线垂直于∠A的平分线于点N,分别交A 2020-05-16 …
直线y=x-3与x轴的交点为A,与y轴的交点为B,抛物线y=ax²+bx+c经过点A,B及点M(- 2020-06-06 …
如图,点P为⊙O外一点,PO及延长线分别交⊙O于A、B,过点P作一直线交⊙O于M、N(异于A、B) 2020-06-17 …
已知E(2,2)是抛物线C:y方=2px上一点,经过点(2,0)的直线l与抛物线C交于A,B两点( 2020-07-26 …
如图过圆O外一点P作该圆的两条割线PAB和PCD分别交圆O于点ABCD弦AD和BC交于Q点,割线P 2020-07-31 …
如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及 2020-11-01 …
在三角形ABC中,AC边上一点D交BC反向延长线为E,且AD=EB,AB交DE于F点,求证EF:FB 2020-12-25 …
1.已知,过正方形ABCD的顶点A作直线交BD于E,交CD于F,交BC的延长线于G,若H是FG的中点 2020-12-30 …