早教吧作业答案频道 -->数学-->
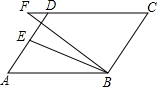
如图,在▱ABCD中,E为AD的中点,F为CD延长线上一点,若∠CFB=2∠ABE.求证:BF=DC-DF.
题目详情
如图,在▱ABCD中,E为AD的中点,F为CD延长线上一点,若∠CFB=2∠ABE.求证:BF=DC-DF.

▼优质解答
答案和解析
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,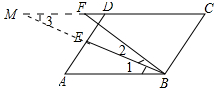
∴∠CFB=∠ABF,
又∵∠CFB=2∠ABE,
∴∠ABF=2∠ABE,
∴BE为∠ABF的角平分线,
∴∠1=∠2,
延长BE交CD的延长线于M,如图所示:
∵AB∥CM,
∴∠1=∠3,
∴∠2=∠3,
∴BF=MF,
∵E我AD的中点,
∴AE=DE,
在△ABE和△DME中,
,
∴△ABE≌△DME(AAS),
∴AB=DM=CD,
∵MF=DM-DF,
∴BF=DC-DF.
∴AB=CD,AB∥CD,

∴∠CFB=∠ABF,
又∵∠CFB=2∠ABE,
∴∠ABF=2∠ABE,
∴BE为∠ABF的角平分线,
∴∠1=∠2,
延长BE交CD的延长线于M,如图所示:
∵AB∥CM,
∴∠1=∠3,
∴∠2=∠3,
∴BF=MF,
∵E我AD的中点,
∴AE=DE,
在△ABE和△DME中,
|
∴△ABE≌△DME(AAS),
∴AB=DM=CD,
∵MF=DM-DF,
∴BF=DC-DF.
看了如图,在▱ABCD中,E为AD...的网友还看了以下:
已知抛物线y=a(x+m)²+k与抛物线y=(x+1)²+3有相同的顶点且经过点A(0,1)①求此 2020-06-05 …
抛物线Y=AX^2-8AX+12A(A<0)与X轴交于A,B两点(点A在点B的左侧),抛物线上另有 2020-06-11 …
在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线 2020-07-09 …
在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A.点A关于直线 2020-07-09 …
空间向量第一题:求点(a,b,c)的关于(1)各坐标面;(2)各坐标轴的对称点的坐标第二题:在yo 2020-07-16 …
在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线 2020-07-20 …
在平面直角坐标系xOy中,点A为第一象限角平分线上一点,点A到x轴的距离为2,点B的y轴正半轴上一 2020-07-30 …
如图,已知抛物线y=-14x2-12x+2与x轴交于A、B两点,与y轴交于点C(1)求点A,B,C 2020-07-30 …
设点A的坐标为(x,y),其中横坐标x可取-1、2,纵坐标y可取-1、1、2.(1)求出点A的坐标 2020-08-01 …
如图1,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED、△DCF分别沿D 2020-11-02 …