早教吧作业答案频道 -->数学-->
如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.(1)求证:△ABE≌△FCE;(2)连接AC、BF,若AE=12BC,求证:四边形ABFC为矩形;(3)在(2
题目详情
如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
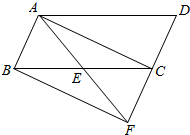
(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE=
BC,求证:四边形ABFC为矩形;
(3)在(2)条件下,直接写出当△ABC再满足___时,四边形ABFC为正方形.

(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE=
| 1 |
| 2 |
(3)在(2)条件下,直接写出当△ABC再满足___时,四边形ABFC为正方形.
▼优质解答
答案和解析
证明:(1)∵四边形ABCD为平行四边形,
∴AB∥DC,
∴∠ABE=∠ECF,
又∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∵
,
∴△ABE≌△FCE(ASA);
(2)∵△ABE≌△FCE,
∴BE=EC,AE=EF,
∴四边形ABFC为平行四边形,
又∵AE=
BC,
∴AF=BC,
∴四边形ABFC为矩形;
(3)当△ABC为等腰三角形时,即AB=AC时,四边形ABFC为正方形;
理由如下:
∵AB=AC,E为BC的中点,
∴AE⊥BC,
∵四边形ABFC为平行四边形,
∴四边形ABFC是菱形,
又∵四边形ABFC是矩形,
∴四边形ABFC为正方形.
故答案为:AB=AC.
∴AB∥DC,
∴∠ABE=∠ECF,
又∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∵
|
∴△ABE≌△FCE(ASA);

(2)∵△ABE≌△FCE,
∴BE=EC,AE=EF,
∴四边形ABFC为平行四边形,
又∵AE=
| 1 |
| 2 |
∴AF=BC,
∴四边形ABFC为矩形;
(3)当△ABC为等腰三角形时,即AB=AC时,四边形ABFC为正方形;
理由如下:
∵AB=AC,E为BC的中点,
∴AE⊥BC,
∵四边形ABFC为平行四边形,
∴四边形ABFC是菱形,
又∵四边形ABFC是矩形,
∴四边形ABFC为正方形.
故答案为:AB=AC.
看了如图,已知E是平行四边形ABC...的网友还看了以下:
已知f(x) 是定义在R 上的不恒为零的函数,且对于任意的 a,b 属于R都满足:f(ab)=af 2020-04-05 …
基本初等函数,在线等已知x∈[-3,2],求f(x)=(1/4X)-(1/2X)+1的最小和最大值 2020-04-27 …
设f(x0在[a,b]单调连续,(a,b)可导,a=f(a)<f(b)=b求证:存在ξi∈(a,b 2020-05-14 …
C语言一道简单的题目An Easy ProblemTime Limit:1000MS Memor 2020-05-16 …
已知函数f(x)在区间(-∝,+∝)上是增函数,a,b∈R求证:若a+b≥0.则f(a)+f(b) 2020-05-17 …
1.f(x)为奇函数在(0,正无穷)为减函数且f(x)0,求k的取值范围3.f(x)是定义在[-1 2020-05-20 …
求证几个函数对称定理!50待加.1.函数f(x)定义域为R.求证y=f(x-m)与y=f(m-x) 2020-06-06 …
已知f(x)=lg(1-x/1+x),a,b∈(-1,1)求证f(a)+f(b)=f[(a+b)/ 2020-07-09 …
已知函数f(x)=log以2为底(1+x)/(1-x)求证;f(x1)+f(x2)=f[(a+b) 2020-07-15 …
原函数积分加反函数积分…我总不可能画个图吧…怎办…原函数f(x)在[a,b]上单调递增,a>0,f( 2020-11-08 …