如图，地面上有一竖直放置的圆形标志物，圆心为C，与地面的接触点为G．与圆形标志物在同一平面内的地面上点P处有一个观测点，且PG=50m．在观测点正前方10m处（即PD=10m）有一个高为10m（

Question

如图，地面上有一竖直放置的圆形标志物，圆心为C，与地面的接触点为G．与圆形标志物在同一平面内的地面上点P处有一个观测点，且PG=50m．在观测点正前方10m处（即PD=10m）有一个高为10m（即ED=10m）的广告牌遮住了视线，因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧．

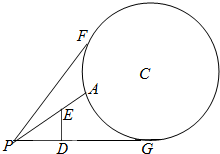
（1）若圆形标志物半径为25m，以PG所在直线为x轴，G为坐标原点，建立直角坐标系，求圆C和直线PF的方程；
（2）若在点P处观测该圆形标志的最大视角（即∠APF）的正切值为(41)/(39)，求该圆形标志物的半径．

Answer 1

（1）圆C：x²+（y-25）²=25²．
直线PB方程：x-y+50=0．
设直线PF方程：y=k（x+50）（k>0），
因为直线PF与圆C相切，所以(|25+50k|)/(√(1+k2))=25，解得k=(4)/(3)…（6分）
所以直线PF方程：y=(4)/(3)(x+50)，即4x-3y+200=0…（8分）
（2）设直线PF方程：y=k（x+50）（k>0），圆C：x²+（y-r）²=r²．
因为tan∠APF=tan（∠GPF-∠GPA）=(k-1)/(1+k)=(41)/(39)，所以k=(40)/(9)…（10分）
所以直线PF方程：y=(40)/(9)(x+50)，即40x-9y+2000=0．
因为直线PF与圆C相切，所以(|9r-2000|)/(√(1600+81))=r，…（13分）
化简得2r²+45r-5000=0，即（2r+125）（r-40）=0．
故r=40…（16分）