早教吧作业答案频道 -->数学-->
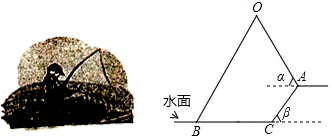
小州在堤边垂钓,如图1,钓竿OA的倾斜角α为60°,河堤AC的坡角β为45°,且AC=2米,AO=4米,钓竿AO与钓鱼线OB的夹角为60°,其中浮漂在点B处,如图2.(1)求点O到水面的垂直距离.(2)求浮
题目详情
小州在堤边垂钓,如图1,钓竿OA的倾斜角α为60°,河堤AC的坡角β为45°,且AC=2米,AO=4米,钓竿AO与钓鱼线OB的夹角为60°,其中浮漂在点B处,如图2.
(1)求点O到水面的垂直距离.
(2)求浮漂B与河堤点C之间的距离.
(1)求点O到水面的垂直距离.
(2)求浮漂B与河堤点C之间的距离.

▼优质解答
答案和解析
(1)作OD⊥BC于D,AF⊥BC于F,AE⊥OD于E,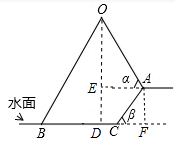
∵河堤AC的坡角β为45°,
∴AF=CF=AC×sin∠ACF=
,
∵钓竿OA的倾斜角α为60°,
∴OE=OA×sin∠OAE=2
,AE=2,
则OD=OE+DE=OE+AF=
+2
,
答:点O到水面的垂直距离为(
+2
)米;
(2)由题意得,∠BOD=30°,
∴BD=OD×tan30°=
+2,
∴BC=BD+AE-CF=
+4-
,
答:浮漂B与河堤点C之间的距离为(
+4-
)米.

∵河堤AC的坡角β为45°,
∴AF=CF=AC×sin∠ACF=
| 2 |
∵钓竿OA的倾斜角α为60°,
∴OE=OA×sin∠OAE=2
| 3 |
则OD=OE+DE=OE+AF=
| 2 |
| 3 |
答:点O到水面的垂直距离为(
| 2 |
| 3 |
(2)由题意得,∠BOD=30°,
∴BD=OD×tan30°=
| ||
| 3 |
∴BC=BD+AE-CF=
| ||
| 3 |
| 2 |
答:浮漂B与河堤点C之间的距离为(
| ||
| 3 |
| 2 |
看了小州在堤边垂钓,如图1,钓竿O...的网友还看了以下:
椭圆X^2/a^2+y^2/b^2=1(a>b>0)的一个焦点是F(1,0),O为坐标原点.设过点 2020-05-16 …
已知a大于等于0,函数f(x)=x^2+ax.设x1属于(负无穷,-a/2),记曲线y=f(x)在 2020-05-23 …
已知p(-1,0),o为原点,角poq=150°,pq=2,则q点坐标为? 2020-06-02 …
已知曲线C上的任意一点P到两个定点F1(-根3,0),和F2(根3,0)的距离和是4.求曲线C的方 2020-06-03 …
已知三个向量与它们的坐标,要证明这三个向量在同一条直线上怎么证?忘了…这道题是这样的:OA=(1, 2020-07-10 …
2,已知正比例函数Y=4x的图象有一点P(X,Y)点A是(6,0),o为坐标原点三角形PAO的面积 2020-08-01 …
已知点A(1,0),o为坐标原点,P的坐标(x,y)满足y=x^2+1,则向量OA在向量OP方向上 2020-08-02 …
A1、A2为x2/a2+y2/b2=1)左右顶点椭圆丄异于A1A2的P,向量POPA=0求椭圆离心 2020-08-02 …
已知点P(-1,0),O为原点,∠POQ=150度,PQ=2,则点Q坐标为何? 2020-08-02 …
在直角坐标系中,ΔABO的顶点A坐标为A(6,0),O为原点,AB=8,∠BAO=60度,ΔABO绕 2020-11-04 …