早教吧作业答案频道 -->数学-->
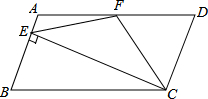
如图,在平行四边形ABCD中,AD=2CD,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=∠ECF;②EF=CF;③∠DFE=3∠AEF;④S△BEC<2S△CEF.中一定成立的是.(请填序号
题目详情
如图,在平行四边形ABCD中,AD=2CD,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=∠ECF;②EF=CF;③∠DFE=3∠AEF;④S△BEC<2S△CEF.中一定成立的是___.(请填序号)

▼优质解答
答案和解析
如图延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.
∵四边形ABCD是平行四边形,
∴AB∥CH,
∴∠A=∠FDH,
在△AFE和△DFH中,
,
∴△AFE≌△DFH,
∴EF=FH,
∵CE⊥AB,AB∥CH,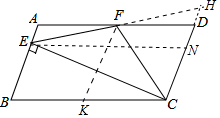
∴CE⊥CD,
∴∠ECH=90°,
∴CF=EF=FH,故②正确,
∵DF=CD=AF,
∴∠DFC=∠DCF=∠FCB,
∵∠FCB>∠ECF,
∴∠DCF>∠ECF,故①错误,
易证四边形DFKC是菱形,
∴∠DFC=∠KFC,
∵AE∥EK,
∴∠AEF=∠EFK,
∵FE=FC,FK⊥EC,
∴∠EFK=∠KFC,
∴∠DFE=3∠AEF,故③正确,
∵四边形EBCN是平行四边形,
∴S△BEC=S△ENC,
∵S△EHC=2S△EFC,S△EHC>S△ENC,
∴S△BEC<2S△CEF,故④正确,
故正确的有②③④.
故答案为②③④.
∵四边形ABCD是平行四边形,
∴AB∥CH,
∴∠A=∠FDH,
在△AFE和△DFH中,
|
∴△AFE≌△DFH,
∴EF=FH,
∵CE⊥AB,AB∥CH,

∴CE⊥CD,
∴∠ECH=90°,
∴CF=EF=FH,故②正确,
∵DF=CD=AF,
∴∠DFC=∠DCF=∠FCB,
∵∠FCB>∠ECF,
∴∠DCF>∠ECF,故①错误,
易证四边形DFKC是菱形,
∴∠DFC=∠KFC,
∵AE∥EK,
∴∠AEF=∠EFK,
∵FE=FC,FK⊥EC,
∴∠EFK=∠KFC,
∴∠DFE=3∠AEF,故③正确,
∵四边形EBCN是平行四边形,
∴S△BEC=S△ENC,
∵S△EHC=2S△EFC,S△EHC>S△ENC,
∴S△BEC<2S△CEF,故④正确,
故正确的有②③④.
故答案为②③④.
看了如图,在平行四边形ABCD中,...的网友还看了以下:
如图,△ABC中,D、E分别是AB,AC边上的中点,连接DE并延长使EF=DE,连接DC、CF、A 2020-04-09 …
8、如图888888,已知,A、D、B、C、在同一直线上,AB=CD,AE=DF,BE=CE,那么 2020-04-25 …
相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE,EF.有下列四 2020-05-13 …
如图,△ABC是等边三角形,点D、E、F分别是线段AB、BC、CA上的点,(1)若AD=BE=CF 2020-05-13 …
(2014•东海县一模)已知:如图,在△ABC中,∠ACB=90°,∠CAB的平分线交BC于D,D 2020-05-13 …
如图,在Rt△ABC中,∠ACB=90°,点E在AB上,AE=AC,过E点作EF垂直于CE交BC于 2020-05-13 …
已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.若四边形ABCD是平行四 2020-05-16 …
BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,且CE=BF,求证:AD平分∠BAC? 2020-05-17 …
已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.(1)若AB=3 2020-05-17 …
如图,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E顺时针旋转180°得到△ 2020-05-23 …