早教吧作业答案频道 -->数学-->
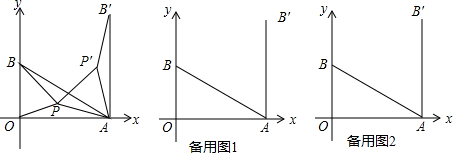
如图,在平面直角坐标系中A(3,0),B(0,1),点P为△OAB内任一点,连PO、PA、PB,将△ABP绕着点A顺时针旋转60°得到△AB′P′,连PP′.(1)求点B′的坐标;(2)当△OPA与△APB满足什么
题目详情
如图,在平面直角坐标系中A(
,0),B(0,1),点P为△OAB内任一点,连PO、PA、PB,将△ABP绕着点A顺时针旋转60°得到△AB′P′,连PP′.
(1)求点B′的坐标;
(2)当△OPA与△APB满足什么条件时,PO+PA+PB的值最小,并求出此最小值;
(3)试直接写出(2)中的点P坐标.
| 3 |
(1)求点B′的坐标;
(2)当△OPA与△APB满足什么条件时,PO+PA+PB的值最小,并求出此最小值;
(3)试直接写出(2)中的点P坐标.

▼优质解答
答案和解析
(1)∵A(
,0),B(0,1)
∴AB=2,∠BAO=30°
∵将△ABP绕着点A顺时针旋转60°得到△AB′P′
∴AB′=2,∠B′AO=90°
∴B′(
,2)
(2)由旋转可得,△APP′是等边三角形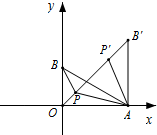
∴PP′=PA
又∵P′B′=PB
∴PO+PA+PB=PO+PP′+P′B′
∴如图,当O、P、P′、B′四点共线时,PO+PA+PB的值最小
∴当∠OPA=∠APB=∠AP′B′=120°时,PO+PA+PB的值最小
此时,PO+PA+PB=OB′=
=
(3)如图,将(2)中的△OPB绕着点O逆时针旋转60°得到△OB″P″,则∠BOB″=60°,OB″=OB=1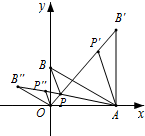
∴点B的坐标为(-
,
)
由(2)可知A、P、P″、B″四点共线
∴点P为OB′与AB″的交点
根据A、B″两点的坐标可得直线AB″的解析式为y=-
x+
根据B′的坐标可得直线OB′的解析式为y=
x
联立方程组,解得P(
,
| 3 |
∴AB=2,∠BAO=30°
∵将△ABP绕着点A顺时针旋转60°得到△AB′P′
∴AB′=2,∠B′AO=90°
∴B′(
| 3 |
(2)由旋转可得,△APP′是等边三角形

∴PP′=PA
又∵P′B′=PB
∴PO+PA+PB=PO+PP′+P′B′
∴如图,当O、P、P′、B′四点共线时,PO+PA+PB的值最小
∴当∠OPA=∠APB=∠AP′B′=120°时,PO+PA+PB的值最小
此时,PO+PA+PB=OB′=
22+(
|
| 7 |
(3)如图,将(2)中的△OPB绕着点O逆时针旋转60°得到△OB″P″,则∠BOB″=60°,OB″=OB=1

∴点B的坐标为(-
| ||
| 2 |
| 1 |
| 2 |
由(2)可知A、P、P″、B″四点共线
∴点P为OB′与AB″的交点
根据A、B″两点的坐标可得直线AB″的解析式为y=-
| ||
| 9 |
| 1 |
| 3 |
根据B′的坐标可得直线OB′的解析式为y=
2
| ||
| 3 |
联立方程组,解得P(
| ||
| 7 |
看了如图,在平面直角坐标系中A(3...的网友还看了以下:
在一张长方形ABCD纸片中,AD=25cm,AB=20cm,现在将这张纸片按下列图片方程式折叠,请分 2020-03-31 …
如图1,点为直线AB上一点,过点O做射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点 2020-05-16 …
如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角形的直角顶点放在 2020-05-16 …
如图,在△ABC中,∠A=90°,AB=AC,D为BC中点(1)如图1,点E、F分别是AB、AC上 2020-05-24 …
某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.如图1,点P为线段AB上的一个动点,分别以 2020-06-11 …
元旦捧回家!1、如图1,点C在线段AB上,点M、N分别是线段AB、AC的中点,MN=3cm,AC= 2020-06-25 …
分式不等式的否命题是否等价于其否定不等式的解集,如P:1/(x-2)2或者是P的解集的其它部分:x 2020-07-14 …
数列极限题,用p(n)表示n的质因数个数,例如p(1)=0,p(2)=1,p(3)=1,p(4)= 2020-07-31 …
在一张长方形ABCD纸片中,AD=8cm,AB=6cm,现将这张纸片按下列图示方法折叠请解决下列问 2020-08-01 …
如图1,点P,Q分别是边长为4CM的等边三角形ABC边AB,BC的动点,点P从顶点A,点Q从顶点B同 2020-11-04 …