早教吧作业答案频道 -->数学-->
对于函数y=f(x),若其定义域内存在不同实数x1,x2,使得xif(xi)=1(i=1,2)成立,则称函数f(x)具有性质P,若函数f(x)=exa具有性质P,则实数a的取值范围为.
题目详情
对于函数y=f(x),若其定义域内存在不同实数x1,x2,使得xif(xi)=1(i=1,2)成立,则称函数f(x)具有性质P,若函数f(x)=
具有性质P,则实数a的取值范围为___.
| ex |
| a |
▼优质解答
答案和解析
由题意知:若f(x)具有性质P,
则在定义域内xf(x)=1有两个不同的实数根,
∵f(x)=
,∴x•
=1,
即方程xex=a在R上有两个不同的实数根,
设g(x)=xex,则g′(x)=ex+xex=(1+x)ex,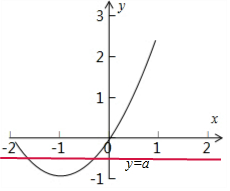
由g′(x)=0得,x=-1,
∴g(x)在(-∞,-1)上递减,在(-1,+∞)上递增,
∴当x=-1时,g(x)取到最小值是g(-1)=-
,
∵x<0,g(x)<0、x>0,g(x)>0,
∴当方程xex=a在R上有两个不同的实数根时,
即函数g(x)与y=a的图象有两个交点,
由图得-
<a<0,
∴实数a的取值范围为(-
,0),
故答案为:(-
,0).
则在定义域内xf(x)=1有两个不同的实数根,
∵f(x)=
| ex |
| a |
| ex |
| a |
即方程xex=a在R上有两个不同的实数根,
设g(x)=xex,则g′(x)=ex+xex=(1+x)ex,

由g′(x)=0得,x=-1,
∴g(x)在(-∞,-1)上递减,在(-1,+∞)上递增,
∴当x=-1时,g(x)取到最小值是g(-1)=-
| 1 |
| e |
∵x<0,g(x)<0、x>0,g(x)>0,
∴当方程xex=a在R上有两个不同的实数根时,
即函数g(x)与y=a的图象有两个交点,
由图得-
| 1 |
| e |
∴实数a的取值范围为(-
| 1 |
| e |
故答案为:(-
| 1 |
| e |
看了对于函数y=f(x),若其定义...的网友还看了以下:
f(x)在[0,4]连续可导,且f(0)=0,f(1)=1,f(4)=2,证明存在a使得f''(a 2020-05-14 …
帮忙做道微积分题吧...大一的...设函数f(x)在[0,a]上连续,在(0,a)内可导,且f(0 2020-06-11 …
设f(x)在闭区间0,1连续,且f(0)=f(1),证必有一点a属于(0,1),使f(a+0.5) 2020-06-22 …
设f(x)在闭区间0,1连续,且f(0)=f(1),证必有一点a属于(0,1),使f(a+0.5) 2020-06-22 …
数学分析习题.设函数f(x)在[a,b]上三阶可导,证明:存在一点e∈(a,b)设函数f(x)在[ 2020-07-16 …
已知函数f(x)在[0,2]上连续,且有f(0)=f(2),求证:必存在一点必存在一点a属于[0, 2020-07-27 …
高数证明题设函数f(x)在[-1,1]上具有三阶连续导数,且f(-1)=0,f(1)=1,f`(0 2020-07-30 …
函数f(0)+f(1)+f(2)=3f(3)=1证明f'(x)=0设函数f(x)在[0,3]上连续 2020-08-02 …
设函数f(x)在[a,b]上三阶可导,证明:存在一点e∈(a,b),使得f(b)=f(a)+1/2 2020-08-02 …
f(x)在[0,1]上可导,f(0)=0,f(1)=1,且f(x)不恒等于x.证明存在a∈(0,1) 2020-11-08 …