早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧).(1)求该抛物线的表达式及点B,C的坐标;(2)抛物线的对称轴与x轴交于点D,若直线y=
题目详情
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧).
(1)求该抛物线的表达式及点B,C的坐标;
(2)抛物线的对称轴与x轴交于点D,若直线y=kx+b经过点D和点E(-1,-2),求直线DE的表达式;
(3)在(2)的条件下,已知点P(t,0),过点P作垂直于x轴的直线交抛物线于点M,交直线DE于点N,若点M和点N中至少有一个点在x轴下方,直接写出t的取值范围.

(1)求该抛物线的表达式及点B,C的坐标;
(2)抛物线的对称轴与x轴交于点D,若直线y=kx+b经过点D和点E(-1,-2),求直线DE的表达式;
(3)在(2)的条件下,已知点P(t,0),过点P作垂直于x轴的直线交抛物线于点M,交直线DE于点N,若点M和点N中至少有一个点在x轴下方,直接写出t的取值范围.
▼优质解答
答案和解析
(1)∵抛物线y=mx2-2mx+m+4与y轴交于点A(0,3),
∴m+4=3.
∴m=-1.
∴抛物线的表达式为y=-x2+2x+3.
∵抛物线y=-x2+2x+3与x轴交于点B,C,
∴令y=0,即-x2+2x+3=0.
解得 x1=-1,x2=3.
又∵点B在点C左侧,
∴点B的坐标为(-1,0),点C的坐标为(3,0);
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线的对称轴为直线x=1.
∵抛物线的对称轴与x轴交于点D,
∴点D的坐标为(1,0).
∵直线y=kx+b经过点D(1,0)和点E(-1,-2),
∴
解得
∴直线DE的表达式为y=x-1;
(3)如图,当P点在D、B两点之间时,M、N都在x轴上方,
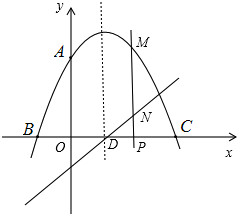
∴点M、N至少有一个点在x轴下方的t的范围为:t<1或t>3.
∴m+4=3.
∴m=-1.
∴抛物线的表达式为y=-x2+2x+3.
∵抛物线y=-x2+2x+3与x轴交于点B,C,
∴令y=0,即-x2+2x+3=0.
解得 x1=-1,x2=3.
又∵点B在点C左侧,
∴点B的坐标为(-1,0),点C的坐标为(3,0);
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线的对称轴为直线x=1.
∵抛物线的对称轴与x轴交于点D,
∴点D的坐标为(1,0).
∵直线y=kx+b经过点D(1,0)和点E(-1,-2),
∴
|
解得
|
∴直线DE的表达式为y=x-1;
(3)如图,当P点在D、B两点之间时,M、N都在x轴上方,

∴点M、N至少有一个点在x轴下方的t的范围为:t<1或t>3.
看了在平面直角坐标系xOy中,抛物...的网友还看了以下:
如图,在平面直角坐标系xOy中,抛物线y=2mx2-2x与x轴负半轴交于点A,顶点为B,且对称轴与 2020-05-13 …
如图,在直角坐标系中,M为X轴上一点,⊙M交X轴于A,B两点,交Y轴于C,D两点,P为BC弧上的一 2020-05-16 …
(2006•深圳)如图1,在平面直角坐标系xOy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点, 2020-06-14 …
如图1,在平面直角坐标系xoy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点 2020-06-14 …
如图,圆与坐标轴交于点.⑴求与直线垂直的圆的切线方程;⑵设点是圆上任意一点(不在坐标轴上),直线交 2020-06-15 …
如图,在平面直角坐标系中,点A在x轴负半轴上,点B的坐标是(0,2),过点B作BC⊥AB交x轴于点 2020-07-20 …
已知抛物线y=x2-px+p2-14(1)若抛物线与y轴交点的坐标为(0,1),求抛物线与x轴交点 2020-07-29 …
如图,在平面直角坐标系内,点o为原点坐标,经过点A(2,6)的直线交x轴负半轴于点B,交Y轴于点C 2020-07-29 …
如图,在平面直角坐标系内,点0为坐标原点,经过点A(2,6)的直线交x轴负半轴于点B,交y轴于点C 2020-08-02 …
如图1,在平面直角坐标系中,直线AB交X轴于点A,交Y轴于B点,点C是直线AB上一动点如图1,在平面 2020-11-02 …