如图17－10所示，一小球从A点以某一水平向右的初速度出发，沿水平直线轨道运动到B点后，进入半径R＝10cm的光滑竖直圆形轨道，圆形轨道间不相互重叠，即小球离开圆形轨道后

Question

如图17－10所示，一小球从 A 点以某一水平向右的初速度出发，沿水平直线轨道运动到 B 点后，进入半径 R ＝10 cm的光滑竖直圆形轨道，圆形轨道间不相互重叠，即小球离开圆形轨道后可继续向 C 点运动， C 点右侧有一壕沟， C 、 D 两点的竖直高度 h ＝0.8 m，水平距离 s ＝1.2 m，水平轨道 AB 长为 L ₁ ＝1 m， BC 长为 L ₂ ＝3 m，小球与水平轨道间的动摩擦因数 μ ＝0.2，重力加速度 g ＝10 m/s ² ，求：

(1)若小球恰能通过圆形轨道的最高点，求小球在 A 点的初速度？

(2)若小球既能通过圆形轨道的最高点，又不掉进壕沟，求小球在 A 点的初速度的范围是多少？

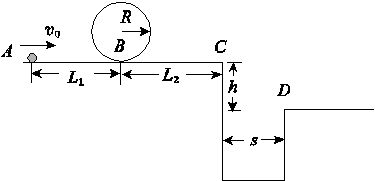
图17－10

Answer 1

解析：(1)对圆周最高点应用牛顿第二定律得 mg＝m 从A点到最高点应用动能定理得 －mg(2R)－μmgL1＝mv－mv， 则A点的速度v0＝3 m/s. (2)若小球恰好停在C处，对全程进行研究，则有 －μmg(L...