早教吧作业答案频道 -->数学-->
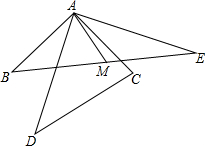
如图所示,∠BAC=∠DAE=90°,M是BE的中点,AB=AC,AD=AE,求证:AM⊥CD.
题目详情
如图所示,∠BAC=∠DAE=90°,M是BE的中点,AB=AC,AD=AE,求证:AM⊥CD.

▼优质解答
答案和解析
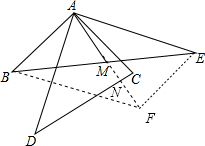 证明:延长AM到F,使MF=AM,交CD于点N,
证明:延长AM到F,使MF=AM,交CD于点N,
∵BM=EM,
∴四边形ABFE是平行四边形,
∴BF=AE,∠ABF+∠BAE=180°,
∵∠BAC=∠DAE=90°,
∴∠CAD+∠BAE=180°,
∴∠ABF=∠CAD,
∵BF=AE,AD=AE,
∴BF=AD,
在△ABF和△CAD中,
,
∴△ABF≌△CAD(SAS),
∴∠BAF=∠ACD,
∵∠BAC=90°,
∴∠BAF+∠CAN=90°,
∴∠ACD+∠CAN=90°,
∴∠ANC=90°,
∴AM⊥CD.
 证明:延长AM到F,使MF=AM,交CD于点N,
证明:延长AM到F,使MF=AM,交CD于点N,∵BM=EM,
∴四边形ABFE是平行四边形,
∴BF=AE,∠ABF+∠BAE=180°,
∵∠BAC=∠DAE=90°,
∴∠CAD+∠BAE=180°,
∴∠ABF=∠CAD,
∵BF=AE,AD=AE,
∴BF=AD,
在△ABF和△CAD中,
|
∴△ABF≌△CAD(SAS),
∴∠BAF=∠ACD,
∵∠BAC=90°,
∴∠BAF+∠CAN=90°,
∴∠ACD+∠CAN=90°,
∴∠ANC=90°,
∴AM⊥CD.
看了 如图所示,∠BAC=∠DAE...的网友还看了以下:
体积相同,pH均等于13的氨水和NaOH溶液.分别加水稀释m倍、n倍,溶液的pH都变成9.则m与n 2020-05-17 …
如图,矩形ABCD中,AD=3厘米,AB=4厘米,N为BC上一点,BN=1厘米,动点M从B点出发, 2020-06-04 …
如图,在四边形ABCD中,AB=CD,AB与CD不平行,M,N分别是AD,BC的中点.则AB与MN 2020-06-12 …
.(本题6分)先阅读下面的内容,例题:若m2+2mn+2n2-6n+9=0,求m和n的值.∵m2+ 2020-07-13 …
已知m,n满足等式(m-8)2+2|n-m+5|=0.(1)求m,n的值;(2)已知线段AB=m, 2020-07-22 …
如图,在平面直角坐标系中,直线y=-34x-3与x轴、y轴分别交于A、B两点,C为x轴正半轴上一点 2020-07-24 …
如图,已知直线l有两条可以左右移动的线段:AB=m,CD=n,且m,n满足|m-4|+(n-8)2 2020-07-25 …
已知a>b>0,全集U=R,集合M={x|b<x<a+b2},N={x|ab<x<a},P={x| 2020-07-30 …
1、已知:实数a、b满足条件a-1的平方根+(ab-2)的平方=0试求1/ab+1/(a+1)(b 2020-08-02 …
如图1,直线AB上,点P在A、B两点之间,点M为线段PB的中点,点N为线段AP的中点,若AB=m,且 2020-11-01 …