早教吧作业答案频道 -->数学-->
如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.(1)求证:△BOC≌△CDA;(2)若AB=2,求阴影部分的面积.
题目详情
如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC为平行四边形.
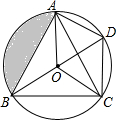
(1)求证:△BOC≌△CDA;
(2)若AB=2,求阴影部分的面积.

(1)求证:△BOC≌△CDA;
(2)若AB=2,求阴影部分的面积.
▼优质解答
答案和解析
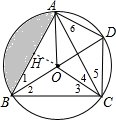 (1)证明:∵O是△ABC的内心,
(1)证明:∵O是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∴AD=CD,
∵四边形OADC为平行四边形,
∴四边形OADC为菱形,
∴BD垂直平分AC,∠4=∠5=∠6,
而∠1=∠5,
∴OA=OC,∠2=∠3,
∴OB=OC,
∴点O为△ABC的外心,
∴△ABC为等边三角形,
∴∠AOB=∠BOC=∠AOC=120°,BC=AC,
∵四边形OADC为平行四边形,
∴∠ADC=∠AOC=120°,AD=OC,CD=OA,
∴AD=OB,
在△BOC和△CDA中
,
∴△BOC≌△CDA;
(2)作OH⊥AB于H,如图,
∵∠AOB=120°,OA=OB,
∴∠BOH=
(180°-120°)=30°,
∵OH⊥AB,
∴BH=AH=
AB=1,
OH=
BH=
,
OB=2OH=
,
∴S阴影部分=S扇形AOB-S△AOB
=
-
×2×
=
.
 (1)证明:∵O是△ABC的内心,
(1)证明:∵O是△ABC的内心,∴∠1=∠2,∠3=∠4,
∴AD=CD,
∵四边形OADC为平行四边形,
∴四边形OADC为菱形,
∴BD垂直平分AC,∠4=∠5=∠6,
而∠1=∠5,
∴OA=OC,∠2=∠3,
∴OB=OC,
∴点O为△ABC的外心,
∴△ABC为等边三角形,
∴∠AOB=∠BOC=∠AOC=120°,BC=AC,
∵四边形OADC为平行四边形,
∴∠ADC=∠AOC=120°,AD=OC,CD=OA,
∴AD=OB,
在△BOC和△CDA中
|
∴△BOC≌△CDA;
(2)作OH⊥AB于H,如图,
∵∠AOB=120°,OA=OB,
∴∠BOH=
| 1 |
| 2 |
∵OH⊥AB,
∴BH=AH=
| 1 |
| 2 |
OH=
| ||
| 3 |
| ||
| 3 |
OB=2OH=
2
| ||
| 3 |
∴S阴影部分=S扇形AOB-S△AOB
=
120•π•(
| ||||
| 360 |
| 1 |
| 2 |
| ||
| 3 |
=
4π-3
| ||
| 9 |
看了 如图,O是△ABC的内心,B...的网友还看了以下:
用所给字母拼成单词.1.a,l,a,d,s.2.a,d,o,s.3.c,o,r,p,n用所给字母拼 2020-05-15 …
设椭圆C:x^2/a^2+y^2/b^2=1(a>b>0)的离心率e=1/2,右焦点到直线x/a+ 2020-05-16 …
A.O(n)B.C.O(nsup>2</sup>)D.O(1) 2020-05-26 …
如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接P 2020-06-13 …
已知椭圆C:x^2/a^2+y^2/b^2=1(a>b>0)已知椭圆C:x^2/a^2+y^2/b 2020-06-14 …
化学物质的比例就等于其下标数吗?比如:C:O=1:2.所以就是CO2?关于化学上,算出一种物质C: 2020-07-09 …
已知以点C(t,2/t)),(t>0)为圆心的圆与与X轴交与O,A,与Y轴交与点O,B其中O为坐标 2020-08-02 …
已知圆O:x^2+y^2=4和C:x^2+(y-4)^2=1(1)判断圆O和圆C的位置关系(2)过圆 2020-11-01 …
刚才你帮我写的这句公式有错误哦!(H-MAX(C,O))>(MIN(C,O)-L)or((H-MAX 2020-11-04 …
已知O(0,0),A(2,1),O,A,B,C依逆时针方向构成正方形的四个顶点.(1)求B,C两点的 2020-12-21 …