早教吧作业答案频道 -->数学-->
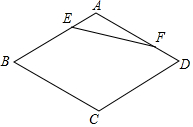
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为.
题目详情
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为___.

▼优质解答
答案和解析
连接AC、CE、CF,如图所示: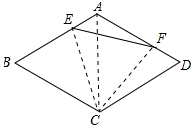
∵四边形ABCD是边长为a的菱形,∠B=60°,
∴△ABC、△CAD都是边长为a的正三角形,
∴AB=BC=CD=AC=AD,∠CAE=∠ACB=∠ACD=∠CDF=60°,
∵AE+AF=a,
∴AE=a-AF=AD-AF=DE,
在△ACE和△DCF中,
,
∴△ACE≌△DCF(SAS),
∴∠ACE=∠DCF,
∴∠ACE+∠ACF=∠DCF+∠ACF,
∴∠ECF=∠ACD=60°,
∴△CEF是正三角形,
∴EF=CE=CF,
当动点E运动到点B或点A时,CE的最大值为a,
当CE⊥AB,即E为BD的中点时,CE的最小值为
a,
∵EF=CE,
∴EF的最小值为
a.
故答案为:
a.

∵四边形ABCD是边长为a的菱形,∠B=60°,
∴△ABC、△CAD都是边长为a的正三角形,
∴AB=BC=CD=AC=AD,∠CAE=∠ACB=∠ACD=∠CDF=60°,
∵AE+AF=a,
∴AE=a-AF=AD-AF=DE,
在△ACE和△DCF中,
|
∴△ACE≌△DCF(SAS),
∴∠ACE=∠DCF,
∴∠ACE+∠ACF=∠DCF+∠ACF,
∴∠ECF=∠ACD=60°,
∴△CEF是正三角形,
∴EF=CE=CF,
当动点E运动到点B或点A时,CE的最大值为a,
当CE⊥AB,即E为BD的中点时,CE的最小值为
| ||
| 2 |
∵EF=CE,
∴EF的最小值为
| ||
| 2 |
故答案为:
| ||
| 2 |
看了 如图,在菱形ABCD中,∠B...的网友还看了以下:
请阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段 2020-04-26 …
在菱形ABCD中,对角线AC,BD交于点O,E为AC上点,且CE=CB,F为BE上点,M为BC上点 2020-05-13 …
(2014•郯城县模拟)如图,在平行四边形ABCD中,E为BC边上的一点,连接AE、BD交于点F, 2020-05-13 …
如图,在菱形ABCD中,∠C=60°,AB=4,过点B作BE⊥CD,垂足为E,连结AE.F为AE上 2020-05-13 …
如图,在菱形ABCD中,∠A=60°,AB=4,O是对角线BD的中点,过O点作OE丄AB,垂足为E 2020-05-13 …
如图,△ABC中,∠BAC=90°,BG平分∠ABC,GF⊥BC于点F,AD⊥BC于点D,交BG于 2020-05-14 …
在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上 2020-06-12 …
(2014•梅州)如图,在Rt△ABC中,∠B=90°,AC=60,AB=30.D是AC上的动点, 2020-06-12 …
如图,把菱形ABCD沿着对角线AC的方向移动到菱形A′B′C′D′的位置,它们的重叠部分(图中阴影 2020-06-13 …
如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.( 2020-06-13 …