早教吧作业答案频道 -->数学-->
已知:直线AB与CD相交于点O.(Ⅰ)如图1,若∠AOM=90°,OC平分∠AOM,则∠AOD=.(Ⅱ)如图2,若∠AOM=90°,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小;(Ⅲ)如图3,若∠AOM=α,∠BOC=4∠B
题目详情
已知:直线AB与CD相交于点O.
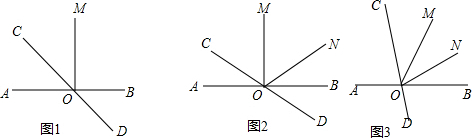
(Ⅰ)如图1,若∠AOM=90°,OC平分∠AOM,则∠AOD=___.
(Ⅱ)如图2,若∠AOM=90°,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小;
(Ⅲ)如图3,若∠AOM=α,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小(用含α的式子表示).
(Ⅰ)如图1,若∠AOM=90°,OC平分∠AOM,则∠AOD=___.
(Ⅱ)如图2,若∠AOM=90°,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小;
(Ⅲ)如图3,若∠AOM=α,∠BOC=4∠BON,OM平分∠CON,求∠MON的大小(用含α的式子表示).

▼优质解答
答案和解析
解(1)∵∠AOM=90°,OC平分∠AOM,
∴∠AOC=
∠AOM=
×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
∠CON=
x°,
∵∠BOM=
x+x=90°,
∴x=36°,
∴∠MON=
x°=
×36°=54°,
即∠MON的度数为54°;
(3)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
∠CON=
x°,
∵∠BOM=
x+x=α,
∴x=
α,
∴∠MON=
×
α=
α.
∴∠AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
| 1 |
| 2 |
| 3 |
| 2 |
∵∠BOM=
| 3 |
| 2 |
∴x=36°,
∴∠MON=
| 3 |
| 2 |
| 3 |
| 2 |
即∠MON的度数为54°;
(3)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB-∠BON=4x°-x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=
| 1 |
| 2 |
| 3 |
| 2 |
∵∠BOM=
| 3 |
| 2 |
∴x=
| 2 |
| 5 |
∴∠MON=
| 3 |
| 2 |
| 2 |
| 5 |
| 3 |
| 5 |
看了 已知:直线AB与CD相交于点...的网友还看了以下:
坐标系中,已知点A(-2,0),B(0,4),C(0,3),过点C交x轴于点D,使得以D,O,C为 2020-06-03 …
三等分角我自己琢磨出一个,自己做的时候能够分出来,请大家帮我瞅瞅:首先画一角AOB,以O为圆点画弧 2020-06-21 …
已知:如图,直线y=−34x+3交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2 2020-06-23 …
如图所示在等腰三角行ABC中,AB=AC,角BAC=50度,角BAC的平分线与AB的中垂线交于点O 2020-07-09 …
如图,AB为圆O的直径,PD切圆O于点C,交AB延长线于点D,且∠D=2∠CAD,(1)求∠D的度 2020-07-14 …
如图,△OAB是边长为2的等边三角形,直线CD经过点A交x轴于点C,交y轴于点D.角ACB=301 2020-07-19 …
(2005•武汉)如图,已知:⊙O1、⊙O2外切于点P,A是⊙O1上一点,直线AC切⊙O2于点C交 2020-07-31 …
∠CEF的度数是多少?求详解在等腰山角形ABC中,AB=AC,∠ABC=50度,∠ABC的平分线与 2020-08-03 …
已知:如图,A,K是圆O上的两点,直线FN垂直于MA,垂足为N,FN与圆O相切与点F,角AOK=2角 2020-10-31 …
在C城周边已有两条公路l1,l2在O点处交汇,且它们的夹角为90度.已知OC=4km,OC与公路l1 2020-12-02 …