如图，射线BD是∠MBN的平分线，点A、C分别是角的两边BM、BN上两点，且AB=BC，E是线段BC上一点，线段EC的垂直平分线交射线BD于点F，连结AE交BD于点G，连结AF、EF、FC．（1）求证：AF=EF；（2）求

Question

如图，射线BD是∠MBN的平分线，点A、C分别是角的两边BM、BN上两点，且AB=BC，E是线段BC上一点，线段EC的垂直平分线交射线BD于点F，连结AE交BD于点G，连结AF、EF、FC．

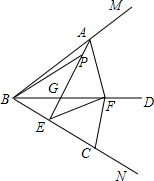
（1）求证：AF=EF；
（2）求证：△AGF∽△BAF；
（3）若点P是线段AG上一点，连结BP，若∠PBG=(1)/(2)∠BAF，AB=3，AF=2，求(EG)/(GP)．

Answer 1

（1）∵BF平分∠ABC，
∴∠ABF=∠CBF．
在△ABF和△CBF中，

BA=BC

∠ABF=∠CBF

BF=BF

，
∴△ABF≌△CBF，
∴AF=CF．
∵点F在EC的垂直平分线上，
∴EF=CF，
∴AF=EF；

（2）∵△ABF≌△CBF，
∴∠BAF=∠BCF．
∵FE=FC，
∴∠FEC=∠FCE，
∴∠BAF=∠FEC．
∵∠BEF+∠FEC=180°，
∴∠BAF+∠BEF=180°．
∵∠BAF+∠ABE+∠BEF+∠AFE=360°，
∴∠ABE+∠AFE=180°．
∵FA=FE，
∴∠FAE=∠FEA．
∵∠AFE+∠FAE+∠FEA=180°，
∴∠ABE=∠FAE+∠FEA=2∠FAE．
又∵∠ABE=2∠ABF，
∴∠FAE=∠ABF．
∵∠AFG=∠BFA，
∴△AGF∽△BAF；

（3）∵△AGF∽△BAF，
∴∠AGF=∠BAF，(FG)/(FA)=(AG)/(BA)．
∵∠PBG=(1)/(2)∠BAF，AB=3，AF=2，
∴∠PBG=(1)/(2)∠AGF，(FG)/(2)=(AG)/(3)，
∴∠BPG=∠PBG，(FG)/(AG)=(2)/(3)，
∴PG=BG，
∴(EG)/(PG)=(EG)/(BG)．
∵∠GAF=∠ABF=∠EBF，∠AGF=∠BGE，
∴△BGE∽△AGF，
∴(GE)/(BG)=(GF)/(AG)=(2)/(3)，
∴(EG)/(PG)=(2)/(3)．