早教吧作业答案频道 -->数学-->
设z是虚数，w＝z＋是实数，且－1＜w＜2，(1)求|z|的值及z的实部的取值范围．(2)设u＝，求证：u为实数．
题目详情
设 z 是虚数， w ＝ z ＋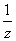 
是实数，且－ 1 ＜ w ＜ 2 ，
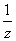是实数，且－ 1 ＜ w ＜ 2 ，
(1) 求 | z | 的值及 z 的实部的取值范围．
(2) 设 u ＝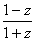 
，求证： u 为实数．
▼优质解答
答案和解析
答案：
解析：
(1)|z|＝1，－＜a＜1 (2)u＝ ∴u为纯虚数
提示：
利用虚数的性质
解析：
(1)|z|＝1，－＜a＜1 (2)u＝ ∴u为纯虚数
提示：
利用虚数的性质
看了 设z是虚数，w＝z＋是实数，...的网友还看了以下：
x＋2y＋z＝e的z次幂求xy偏导数怎么求如题1楼说的是书上普通做法,这题怎么把z倒到一边去啊变形 2020-05-13 …
在数列｛an｝中,al＝2,an＋1＝3an－2n＋1.求数列｛an｝的前n项个Sn 2020-05-15 …
已知根号x＋根号y－1＋根号z－2＝1／2(x＋y＋z),求x,y,z的值. 2020-05-16 …
已知x.y.z为非负有理数,且满足3x＋y＋z＝5,2x＋y－3z＝1,若s＝3x＋y－7z,求s 2020-06-27 …
1.x－y＝5x＋z＝－7y－z＝－82.3x＋2y＋5z＝2x－2y－z＝64x＋2y－7z＝3 2020-07-09 …
已知数列{an}的前n项和Sn＝n的平方＋2n,求数列的通项公式an 2020-07-30 …
三元一次方程组,会的进,聪明的进第一题3x-4y＝4,5x＋2y＋3z＝2,z＝2x-7求x,y, 2020-08-03 …
√（3＋√2＋√3＋√6）＝√x＋√y＋√z,求：xyz的值我没有上多少学女儿问我我就做不想出来 2020-11-01 …
已知复数Z满足：｜Z｜＝1＋3i－Z,求（1＋i＾2）（3＋4i）＾2／2z 2020-11-01 …
设z∈C,则方程(z－2)(－2)＋(z＋2)(＋2)＝2(|z2－4|＋2)表示的曲线是?（高2复 2020-11-03 …