早教吧作业答案频道 -->数学-->
如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.(1)求证:AB⊥平面EDC;(2)若P为FG上任一点,证明:EP∥平面BCD.
题目详情
如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.
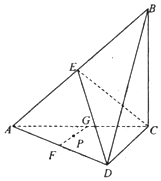
(1)求证:AB⊥平面EDC;
(2)若P为FG上任一点,证明:EP∥平面BCD.

(1)求证:AB⊥平面EDC;
(2)若P为FG上任一点,证明:EP∥平面BCD.
▼优质解答
答案和解析
证明:(1)∵平面ABC⊥平面ACD,∠ACD=90°,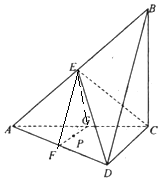
∴CD⊥AC,
∵平面ABC∩平面ACD=AC,CD⊂平面ACD,
∴CD⊥平面ABC,
又AB⊂平面ABC,∴CD⊥AB,
∵AC=BC,E为AB的中点,∴CE⊥AB,
又CE∩CD=C,CD⊂平面EDC,CE⊂平面EDC,
∴AB⊥平面EDC.
(2)连结EF、EG,∵E、F分别为AB、AD的中点,
∴EF∥BD,又BD⊂平面BCD,EF⊄平面BCD,
∴EF∥平面BCD,
同理可EG∥平面BCD,且EF∩EG=E,EF、EG⊂平面BCD,
∴平面EFG∥平面BCD,
∵P是FG上任一点,∴EP⊂平面EFG,
∴EP∥平面BCD.

∴CD⊥AC,
∵平面ABC∩平面ACD=AC,CD⊂平面ACD,
∴CD⊥平面ABC,
又AB⊂平面ABC,∴CD⊥AB,
∵AC=BC,E为AB的中点,∴CE⊥AB,
又CE∩CD=C,CD⊂平面EDC,CE⊂平面EDC,
∴AB⊥平面EDC.
(2)连结EF、EG,∵E、F分别为AB、AD的中点,
∴EF∥BD,又BD⊂平面BCD,EF⊄平面BCD,
∴EF∥平面BCD,
同理可EG∥平面BCD,且EF∩EG=E,EF、EG⊂平面BCD,
∴平面EFG∥平面BCD,
∵P是FG上任一点,∴EP⊂平面EFG,
∴EP∥平面BCD.
看了 如图,在四面体ABCD中,平...的网友还看了以下:
图不能发.在平行四边形ABCD中,角BCD的平分线CE交AD于E,角ABC的平分线BG交CE于F, 2020-05-01 …
谁来帮我做到高三数学题被,如图所示,已知平面α‖平面β‖平面γ,且β位于α与γ之间,点A,D属于平 2020-05-13 …
在三角形ABC中,已知BC=6,BC边上的中线AD=5.点P为线段AD上一点,过P作EF平行于BC 2020-05-24 …
已知,如图,△ABC中,DE是BC的垂直平分线,分别交BC,AC于D,EAB=AD,AD交BE于F 2020-06-06 …
初三数学代数,本人愚钝,想不出来!在三角形ABC中,角ACB为钝角,AD是角BAC的平分线,AD交 2020-06-29 …
四边形ABCD中,AB等于BC.BE垂直于AD垂足为E.角BCD减角ABE等于90度,过点C作CF 2020-07-13 …
如图,AD是△ABC的角平分线,以点C为圆心,CD为半径作圆交BC的延长线于点E,交AD于点F,交 2020-07-21 …
如图,AD是△ABC的角平分线,以点C为圆心,CD为半径作圆交BC的延长线于点E,交AD于点F,交 2020-07-30 …
PA,PB是圆0两切线,PCD是割线,E,F分别在AB,AD上,CE=CF,求证:CF与PA互相平行 2020-12-05 …
如图甲,直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB,已知A 2020-12-25 …