早教吧作业答案频道 -->数学-->
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(Ⅰ)证明MN∥平面PAB;(Ⅱ)求四面体N-BCM的体积.
题目详情
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
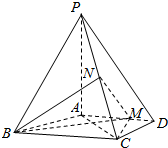
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N-BCM的体积.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N-BCM的体积.
▼优质解答
答案和解析
证明:(Ⅰ)取BC中点E,连结EN,EM,
∵N为PC的中点,∴NE是△PBC的中位线,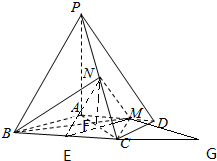
∴NE∥PB,
又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE=
BC=AM=2,
∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,
∵MN⊂平面NEM,∴MN∥平面PAB.
(Ⅱ)取AC中点F,连结NF,
∵NF是△PAC的中位线,
∴NF∥PA,NF=
PA=2,
又∵PA⊥面ABCD,∴NF⊥面ABCD,
如图,延长BC至G,使得CG=AM,连结GM,
∵AM
CG,∴四边形AGCM是平行四边形,
∴AC=MG=3,
又∵ME=3,EC=CG=2,
∴△MEG的高h=
,
∴S△BCM=
×BC×h=
×4×
=2
,
∴四面体N-BCM的体积VN-BCM=
×S△BCM×NF=
×2
×2=
.
∵N为PC的中点,∴NE是△PBC的中位线,

∴NE∥PB,
又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE=
| 1 |
| 2 |
∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,
∵MN⊂平面NEM,∴MN∥平面PAB.
(Ⅱ)取AC中点F,连结NF,
∵NF是△PAC的中位线,
∴NF∥PA,NF=
| 1 |
| 2 |
又∵PA⊥面ABCD,∴NF⊥面ABCD,
如图,延长BC至G,使得CG=AM,连结GM,
∵AM
| ∥ |
. |
∴AC=MG=3,
又∵ME=3,EC=CG=2,
∴△MEG的高h=
| 5 |
∴S△BCM=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
∴四面体N-BCM的体积VN-BCM=
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
4
| ||
| 3 |
看了 如图,四棱锥P-ABCD中,...的网友还看了以下:
己知圆o中EF过圆心o,且垂直于弦AD,B.c两点在直线DE上,且AD平分角BAc.求证DE的平方 2020-04-06 …
圆O中,EF过圆心O,垂直弦AD,B,C在直线DE上,AD平分角BAC,证DE方=BE乘EC 2020-04-06 …
如图,在梯形ABCD中,AD//BC,AB=DC=AD,角C=60度,AE垂直于BD于点E,F是C 2020-05-15 …
如图,在梯形ABCD中,AD//BC,AB=DC=AD,角C=60度,AE垂直于BD于点E,F是C 2020-05-15 …
如图,在等腰梯形ABCD中,AD//BC,BD平分∠ABC (1)求证:AB=AD (2)已知AD 2020-05-16 …
全等三角形的数学题1.AB=AC.BD=CE/角B=角C.证明:AD=AE2.AB//CD.点C是 2020-06-27 …
已知BE和CF是三角形ABC两边上的高,BE=CF,H是BE和CF的交点,求证HB=HC2题已知四 2020-07-15 …
如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD①若∠C=30°,求证:A 2020-07-18 …
三角形余弦定理三角形预选定理中的平面几何证法:在任意△ABC中做AD⊥BC.∠C所对的边为c,∠B 2020-07-30 …
1.如图,AB为圆O的直径C为圆O上的一点,AD和过点C的切线互相垂直,垂足为D,求证:AC平分∠ 2020-08-01 …